Solution to Problem 510 | Flexure Formula
Problem 510
A 50-mm diameter bar is used as a simply supported beam 3 m long. Determine the largest uniformly distributed load that can be applied over the right two-thirds of the beam if the flexural stress is limited to 50 MPa.
- Read more about Solution to Problem 510 | Flexure Formula
- Log in to post comments
Solution to Problem 509 | Flexure Formula
Problem 509
A section used in aircraft is constructed of tubes connected by thin webs as shown in Fig. P-509. Each tube has a cross-sectional area of 0.20 in2. If the average stress in the tubes is no to exceed 10 ksi, determine the total uniformly distributed load that can be supported in a simple span 12 ft long. Neglect the effect of the webs.
- Read more about Solution to Problem 509 | Flexure Formula
- Log in to post comments
Solution to Problem 508 | Flexure Formula
Problem 508
Determine the minimum height h of the beam shown in Fig. P-508 if the flexural stress is not to exceed 20 MPa.
- Read more about Solution to Problem 508 | Flexure Formula
- Log in to post comments
Solution to Problem 507 | Flexure Formula
Problem 507
In a laboratory test of a beam loaded by end couples, the fibers at layer AB in Fig. P-507 are found to increase 60 × 10-3 mm whereas those at CD decrease 100 × 10-3 mm in the 200-mm-gage length. Using E = 70 GPa, determine the flexural stress in the top and bottom fibers.
- Read more about Solution to Problem 507 | Flexure Formula
- Log in to post comments
Solution to Problem 506 | Flexure Formula
Problem 506
A flat steel bar, 1 inch wide by ¼ inch thick and 40 inches long, is bent by couples applied at the ends so that the midpoint deflection is 1.0 inch. Compute the stress in the bar and the magnitude of the couples. Use E = 29 × 106 psi.
- Read more about Solution to Problem 506 | Flexure Formula
- Log in to post comments
Solution to Problem 505 | Flexure Formula
Problem 505
A high strength steel band saw, 20 mm wide by 0.80 mm thick, runs over pulleys 600 mm in diameter. What maximum flexural stress is developed? What minimum diameter pulleys can be used without exceeding a flexural stress of 400 MPa? Assume E = 200 GPa.
- Read more about Solution to Problem 505 | Flexure Formula
- Log in to post comments
Solution to Problem 504 | Flexure Formula
Problem 504
A simply supported beam, 2 in wide by 4 in high and 12 ft long is subjected to a concentrated load of 2000 lb at a point 3 ft from one of the supports. Determine the maximum fiber stress and the stress in a fiber located 0.5 in from the top of the beam at midspan.
- Read more about Solution to Problem 504 | Flexure Formula
- Log in to post comments
Solution to Problem 503 | Flexure Formula
Problem 503
A cantilever beam, 50 mm wide by 150 mm high and 6 m long, carries a load that varies uniformly from zero at the free end to 1000 N/m at the wall. (a) Compute the magnitude and location of the maximum flexural stress. (b) Determine the type and magnitude of the stress in a fiber 20 mm from the top of the beam at a section 2 m from the free end.
- Read more about Solution to Problem 503 | Flexure Formula
- Log in to post comments
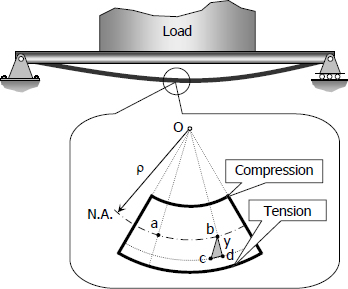
Flexure Formula
- Read more about Flexure Formula
- Log in to post comments