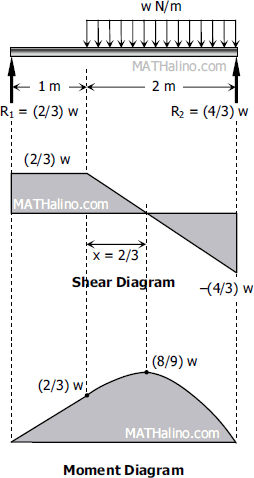
$\Sigma M_{R1} = 0$
$3R_2 = 2w(2)$
$R_2 = \frac{4}{3} w$
$\Sigma M_{R2} = 0$
$3R_1 = 2w(1)$
$R_1 = \frac{2}{3} w$
$(\,f_b\,)_{max} = \dfrac{Mc}{I}$
Where
$(\,f_b\,)_{max} = 50 \, \text{MPa}$
$M = \frac{8}{9} \, \text{N}\cdot\text{m}$
$c = 25 \, \text{mm}$
$I = \dfrac{\pi r^4}{4} = \dfrac{\pi (25^4)}{4}$
$I = 97656.25\pi \, \text{mm}^4$
$50 = \dfrac{\frac{8}{9}w(1000)(25)}{97656.25 \pi}$
$w = 690.29 \, \text{N/m}$
