Solution to Problem 516 | Flexure Formula

Problem 516
A timber beam AB, 6 in wide by 10 in deep and 10 ft long, is supported by a guy wire AC in the position shown in Fig. P-516. The beam carries a load, including its own weight, of 500 lb for each foot of its length. Compute the maximum flexural stress at the middle of the beam.
 

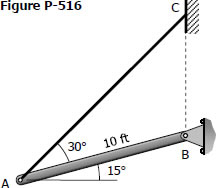
Timber beam supported by guy wire

 

Solution 516
$x = 10 \cos 15^\circ$

$x = 9.66 \, \text{ft}$
 

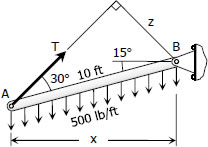516-fbd-for-t.jpg$z = 10 \sin 30^\circ$

$z = 5 \, \text{ft}$
 

$\Sigma M_B = 0$

$zT = 500(10)(x/2)$

$5T = 500(10)(9.66/2)$

$T = 4829.63 \, \text{lb}$
 

At midspan:
$M = T(z/2) - 500(5)(x/4)$

$M = 4829.63(5/2) - 500(5)(9.66/4)$

$M = 6036.58 \, \text{lb}\cdot\text{ft}$
 

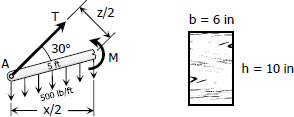
516-fbd-for-m.jpg

 

$f_b = \dfrac{Mc}{I} = \dfrac{M(h/2)}{\dfrac{bh^3}{12}}$

$f_b = \dfrac{6036.58(12)(10/2)}{\dfrac{6(10^3)}{12}}$

$f_b = 724.39 \, \text{psi}$           answer

Tags
Beam
timber
flexural stress