Relevant data from Appendix B, Table B-4 Properties of Channel Sections: SI Units, of
text book.
| Designation |
C200 × 28 |
| Area |
3560 mm2 |
| Width |
64 mm |
| SX-X |
180 × 103 mm3 |
| IY-Y |
0.825 × 106 mm4 |
| x |
14.4 mm |
a. Webs are vertical
$(\,f_b\,)_{max} = \dfrac{M}{S}$
$120 = \dfrac{M}{2(180 \times 10^3 )}$
$M = 43,200,000 \, \text{N}\cdot\text{mm}$
$M = 43.2 \, \text{kN}\cdot\text{m}$
From the figure:
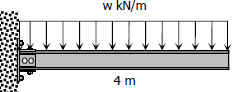$M = 4w(2)$
$M = 8w$
$43.2 = 8w$
$w = 5.4 \, \text{kN/m}$
$w = 550.46 \, \text{kg/m}$
$w = \text{dead load, } DL + \text{live load, } LL$
$550.46 = 2(28) + LL$
$LL = 494.46 \, \text{ kg/m}$ answer
b. Webs are horizontal
$I_{back} = I_{Y-Y} + Ax^2$
$I_{back} = (0.825 \times 10^6) + 3560(14.4^2)$
$I_{back} = 1\,563\,201.6 \, \text{mm}^4$
$I = 2I_{back} = 2(1\,563\,201.6)$
$I = 3\,126\,403.2 \, \text{mm}^4$
$(\,f_b\,)_{max} = \dfrac{Mc}{I}$
$120 = \dfrac{M(64)}{3\,126\,403.2}$
$M = 5\,862\,006 \, \text{N}\cdot\text{mm}$
$M = 5.862 \, \text{kN}\cdot\text{m}$
From the figure:
$M = 4w (2)$
$M = 8w$
$5.862 = 8w$
$w = 0.732\,75 \, \text{kN/m}$
$w = 74.69 \, \text{kg/m}$
$w = \text{dead load, } DL + \text{live load, } LL$
$74.69 = 2(28) + LL$
$LL = 18.69 \, \text{ kg/m}$ answer
