Limit the Deflection of Cantilever Beam by Applying Force at the Free End
Situation
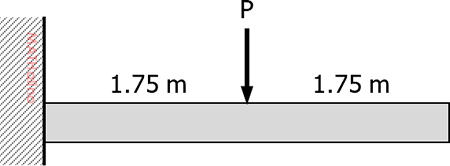
A cantilever beam, 3.5 m long, carries a concentrated load, P, at mid-length.
P = 200 kN
Beam Modulus of Elasticity, E = 200 GPa
Beam Moment of Inertia, I = 60.8 × 106 mm4
1. How much is the deflection (mm) at mid-length?
| A. 1.84 | C. 23.50 |
| B. 29.40 | D. 14.70 |
2. What force (kN) should be applied at the free end to prevent deflection?
| A. 7.8 | C. 62.5 |
| B. 41.7 | D. 100.0 |
3. To limit the deflection at mid-length to 9.5 mm, how much force (kN) should be applied at the free end?
| A. 54.1 | C. 129.3 |
| B. 76.8 | D. 64.7 |