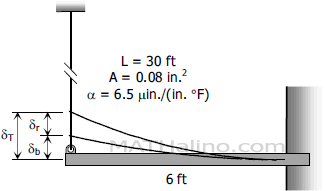
Assuming complete freedom for the rod, the deformation due to drop of temperature is...
$\delta_T = \alpha L \, \Delta T$
$\delta_T = 0.0000065(30)(90)$
$\delta_T = 0.01755 \, \text{ ft} = 0.2106 \, \text{ in.}$
subscript b ( b ) = refers to the beam
subscript r ( r ) = refers to the rod
$\delta_b + \delta_r = \delta_T$
$\left( \dfrac{PL^3}{3EI} \right)_b + \left( \dfrac{PL}{AE} \right)_r = 0.2106$
$\left( \dfrac{PL^3}{3I} \right)_b + \left( \dfrac{PL}{A} \right)_r = 0.2106E$
$\dfrac{P(6^3)(12^3)}{3(154)} + \dfrac{P(30)(12)}{0.08} = 0.2106(29 \times 10^6)$
$807.90P + 4500P = 6\,107\,400$
$5307.9P = 6\,107\,400$
$P = 1150.62 \, \text{ lb} = 1.151 \, \text{ kips}$
Stress increase on the rod
$\sigma = \dfrac{P}{A} = \dfrac{1.151}{0.08}$
$\sigma = 14.39 \, \text{ ksi}$ answer
