$EI ~ t_{A/B} = 0$
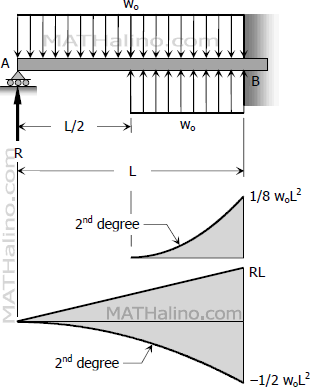
$\frac{1}{3}(\frac{1}{2}L)(\frac{1}{8}w_oL^2)(\frac{7}{8}L) + \frac{1}{2}(L)(RL)(\frac{2}{3}L) - \frac{1}{3}(L)(\frac{1}{2}w_oL^2)(\frac{3}{4}L) = 0$
$\frac{7}{384}w_oL^4 + \frac{1}{3}RL^3 - \frac{1}{8}w_oL^4 = 0$
$\frac{7}{384}w_oL + \frac{1}{3}R - \frac{1}{8}w_oL = 0$
$\frac{1}{3}R = \frac{1}{8}w_oL - \frac{7}{384}w_oL$
$\frac{1}{3}R = \frac{41}{384}w_oL$
$R = \frac{41}{128}w_oL$ answer
$M_{wall} = RL + \frac{1}{8}w_oL^2 - \frac{1}{2}w_oL^2$
$M_{wall} = (\frac{41}{128}w_oL)L + \frac{1}{8}w_oL^2 - \frac{1}{2}w_oL^2$
$M_{wall} = \frac{41}{128}w_oL^2 + \frac{1}{8}w_oL^2 - \frac{1}{2}w_oL^2$
$M_{wall} = -\frac{7}{128}w_oL^2$ answer
