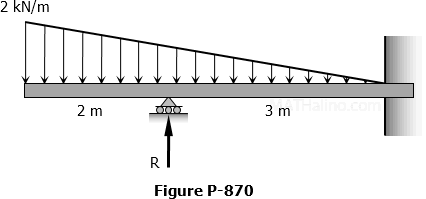
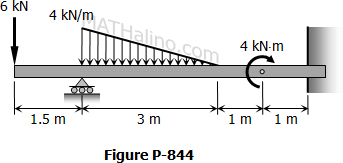
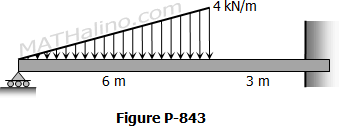
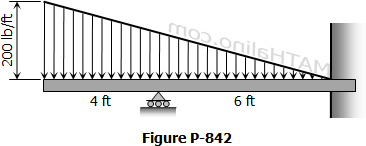
Support Added at the Midspan of Simple Beam to Prevent Excessive Deflection
Situation
A simply supported steel beam spans 9 m. It carries a uniformly distributed load of 10 kN/m, beam weight already included.
Area = 8,530 mm2
Depth = 306 mm
Flange Width = 204 mm
Flange Thickness = 14.6 mm
Moment of Inertia, Ix = 145 × 106 mm4
Modulus of Elasticity, E = 200 GPa
1. What is the maximum flexural stress (MPa) in the beam?
| A. 107 | C. 142 |
| B. 54 | D. 71 |
2. To prevent excessive deflection, the beam is propped at midspan using a pipe column. Find the resulting axial stress (MPa) in the column
Outside Diameter = 200 mm
Thickness = 10 mm
Height, H = 4 m
Modulus of Elasticity, E = 200 GPa
| A. 4.7 | C. 18.8 |
| B. 9.4 | D. 2.8 |
3. How much is the maximum bending stress (MPa) in the propped beam?
| A. 26.7 | C. 15.0 |
| B. 17.8 | D. 35.6 |