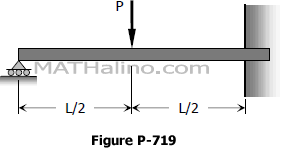
Problem 723 | Propped beam with uniform load over half the span
Problem 723
Find the reaction R and the moment at the wall for the propped beam shown in Fig. P-723.
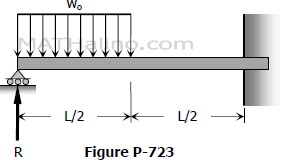
Problem 722 | Propped beam with moment load on the span by area-moment method
Problem 722
For the beam shown in Fig. P-722, compute the reaction R at the propped end and the moment at the wall. Check your results by letting b = L and comparing with the results in Problem 707.
Solution
Problem 719 | Propped beam with concentrated load at midspan by moment-area method
Problem 719
For the propped beam shown in Fig. P-719, determine the propped reaction R and the midspan value of EIδ.
Problem 707 | Propped beam with moment load at simple support by moment-area method
Problem 707
For the propped beam shown in Fig. P-707, solved for vertical reaction R at the simple support.
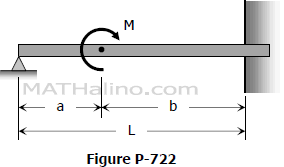
Problem 721 | Propped beam with decreasing load by moment-area method
Problem 721
By the use of moment-are method, determine the magnitude of the reaction force at the left support of the propped beam in Fig. P-706.
Problem 720 | Propped beam with increasing load by moment-area method
Problem 720
Find the reaction at the simple support of the propped beam shown in Fig. P-705 by using moment-area method.
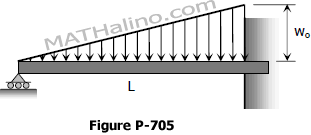
Problem 704 | Propped beam with some uniform load by moment-area method
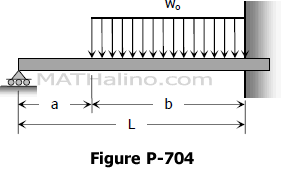
Problem 704
Find the reaction at the simple support of the propped beam shown in Figure PB-001 by using moment-area method.
Application of Area-Moment Method to Restrained Beams
See deflection of beam by moment-area method for details.
Rotation of beam from A to B
Deviation of B from a tangent line through A
- Read more about Application of Area-Moment Method to Restrained Beams
- Log in or register to post comments
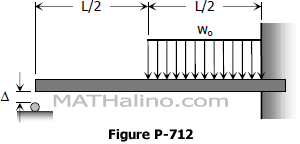
Problem 712 | Propped beam with initial clearance at the roller support
Problem 712
There is a small initial clearance D between the left end of the beam shown in Fig. P-712 and the roller support. Determine the reaction at the roller support after the uniformly distributed load is applied.
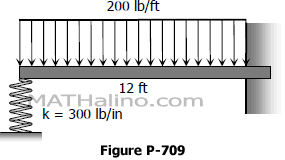
Problem 709 | Propped Beam with Spring Support
Example 06
The beam in Figure PB-006 is supported at the left by a spring that deflects 1 inch for each 300 lb. For the beam E = 1.5 × 106 psi and I = 144 in4. Compute the deflection of the spring.
- Read more about Problem 709 | Propped Beam with Spring Support
- Log in or register to post comments