Problem 733 | Cantilever beam with moment load at the free end and supported by a rod at midspan

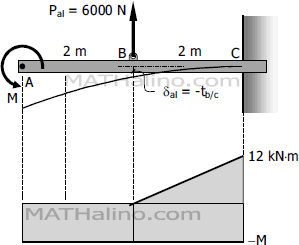
For the aluminum rod
$P_{al} = (\sigma A)_{al}$

$P_{al} = 150(40)$

$P_{al} = 6000 \, \text{ N}$
 

$\delta_{al} = \left( \dfrac{\sigma L}{E} \right)_{al}$

$\delta_{al} = \dfrac{150(5)(1000)}{70\,000}$

$\delta_{al} = \frac{75}{7} \, \text{ mm}$
 

For the steel beam
$t_{B/C} = \dfrac{1}{(EI)_{st}}(\text{Area}_{BC}) \cdot \bar{X}_B$

$t_{B/C} = \dfrac{1}{200\,000(50 \times 10^6)}\left[ \frac{1}{2}(2)(12\,000)(\frac{4}{3} - 2M) \right](1000^3)$

$t_{B/C} = \frac{1}{10\,000}(16\,000 - 2M)$

$t_{B/C} = \frac{8}{5} - \frac{1}{5000}M$
 

From the figure
$\delta_{al} = -t_{B/C}$

$\frac{75}{7} = -(\frac{8}{5} - \frac{1}{5000}M)$

$\frac{1}{5000}M = \frac{431}{35}$

$P = 61\,571.43 \, \text{ N}$

$P = 61.57 \, \text{ kN}$           answer