Problem 731 | Cantilever beam supported by cable at the free-end
Problem 731
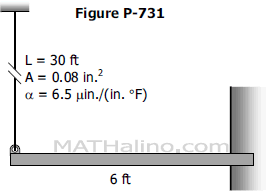
The beam shown in Fig. P-731 is connected to a vertical rod. If the beam is horizontal at a certain temperature, determine the increase in stress in the rod if the temperature of the rod drops 90°F. Both the beam and the rod are made of steel with E = 29 × 106 psi. For the beam, use I = 154 in.4