Solution to Problem 669 | Deflections in Simply Supported Beams

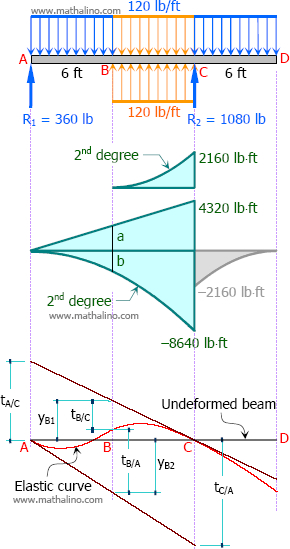
$\Sigma M_{R2} = 0$

$12R_1 + 3(6)(120) = 9(6)(120)$

$R_1 = 360 \, \text{ lb}$
 

$\Sigma M_{R1} = 0$

$12R_2 = 3(6)(120) + 15(6)(120)$

$R_2 = 1080 \, \text{ lb}$
 

By ratio and proportion:
$\dfrac{a}{6} = \dfrac{4320}{12}$

$a = 2160 \, \text{ lb}\cdot\text{ft}$
 

By squared property of parabola:
$\dfrac{b}{6^2} = \dfrac{-8640}{12^2}$

$b = -2160 \, \text{ lb}\cdot\text{ft}$
 

$EI \, t_{C/A} = (Area_{AC}) \, \bar{X}_C$

$EI \, t_{C/A} = \frac{1}{3}(6)(2160)(\frac{3}{2}) + \frac{1}{2}(12)(4320)(4) - \frac{1}{3}(12)(8640)(3)$

$EI \, t_{C/A} = 6480 \, \text{ lb}\cdot\text{ft}^3$
 

$EI \, t_{B/A} = (Area_{AB}) \, \bar{X}_B$

$EI \, t_{B/A} = \frac{1}{2}(6a)(2) - \frac{1}{3}(6b)(\frac{3}{2})$

$EI \, t_{B/A} = 6a - 3b$

$EI \, t_{B/A} = 6(2160) - 3(2160)$

$EI \, t_{B/A} = 6480 \, \text{ lb}\cdot\text{ft}^3$
 

With the values of EI t_C/A and EI t_B/A, it is obvious that the elastic curve is above point B. The deflection at B (up or down) can also be determined by comparing the values of t_B/A and y_B2.
 

By ratio and proportion:
$\dfrac{y_{B2}}{6} = \dfrac{t_{C/A}}{12}$

$y_{B2} = \frac{1}{2}t_{C/A}$

$EI \, y_{B2} = \frac{1}{2}EI \, t_{C/A}$

$EI \, y_{B2} = \frac{1}{2}(6480)$

$EI \, y_{B2} = 3240 \, \text{ lb}\cdot\text{ft}^3$
 

Since t_B/A is greater than y_B2, the elastic curve is above point B as concluded previously.
 

Therefore,
$EI \, \delta_B = EI \, t_{B/A} - EI \, y_{B2}$

$EI \, \delta_B = 6480 - 3240$

$EI \, \delta_B = 3240 \, \text{ lb}\cdot\text{ft}^3$           answer
 

You can also find the value EI δ_B by finding t_A/C, t_B/C, and y_B1. I encourage you to do it yourself.