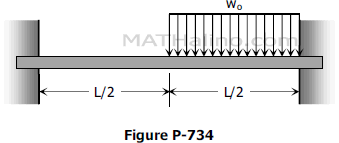
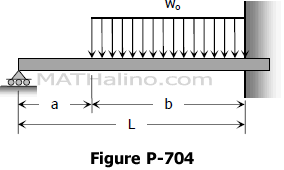
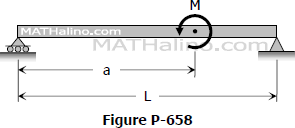
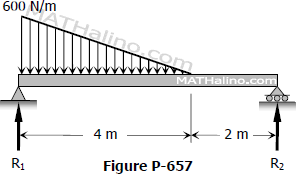
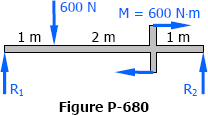
Problem 738 | Fully restrained beam with moment load
Problem 738
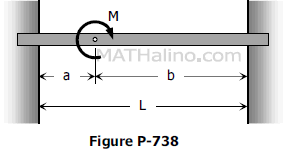
A perfectly restrained beam is loaded by a couple M applied where shown in Fig. P-738. Determine the end moments.
Solution 738
moment diagram by parts
Problem 734 | Restrained beam with uniform load over half the span
Problem 734
Determine the end moments for the restrained beams shown in Fig. P-734.
Problem 722 | Propped beam with moment load on the span by area-moment method
Problem 722
For the beam shown in Fig. P-722, compute the reaction R at the propped end and the moment at the wall. Check your results by letting b = L and comparing with the results in Problem 707.
Solution
Problem 707 | Propped beam with moment load at simple support by moment-area method
Problem 707
For the propped beam shown in Fig. P-707, solved for vertical reaction R at the simple support.
Problem 721 | Propped beam with decreasing load by moment-area method
Problem 721
By the use of moment-are method, determine the magnitude of the reaction force at the left support of the propped beam in Fig. P-706.
Problem 720 | Propped beam with increasing load by moment-area method
Problem 720
Find the reaction at the simple support of the propped beam shown in Fig. P-705 by using moment-area method.
Problem 704 | Propped beam with some uniform load by moment-area method
Problem 704
Find the reaction at the simple support of the propped beam shown in Figure PB-001 by using moment-area method.
Problem 658 | Beam Deflection by Conjugate Beam Method
Problem 658
For the beam shown in Fig. P-658, find the value of EIδ at the point of application of the couple.
Problem 657 | Beam Deflection by Conjugate Beam Method
Problem 657
Determine the midspan value of EIδ for the beam shown in Fig. P-657.
Solution to Problem 680 | Midspan Deflection
Problem 680
Determine the midspan value of EIδ for the beam loaded as shown in Fig. P-680.
- Read more about Solution to Problem 680 | Midspan Deflection
- Log in to post comments