moment diagram by parts
Solution to Problem 674 | Midspan Deflection
Problem 674
Find the deflection midway between the supports for the overhanging beam shown in Fig. P-674.

- Read more about Solution to Problem 674 | Midspan Deflection
- Log in or register to post comments
Solution to Problem 669 | Deflections in Simply Supported Beams
Problem 669
Compute the value of EIδ midway between the supports of the beam shown in Fig. P-669.

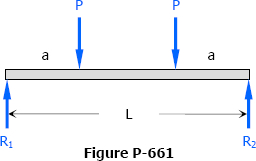
Solution to Problem 661 | Deflections in Simply Supported Beams
Problem 661
Compute the midspan deflection of the symmetrically loaded beam shown in Fig. P-661. Check your answer by letting a = L/2 and comparing with the answer to Problem 609.
Solution to Problem 660 | Deflections in Simply Supported Beams
Problem 660
A simply supported beam is loaded by a couple M at its right end, as shown in Fig. P-660. Show that the maximum deflection occurs at x = 0.577L.

Solution to Problem 659 | Deflections in Simply Supported Beams
Problem 659
A simple beam supports a concentrated load placed anywhere on the span, as shown in Fig. P-659. Measuring x from A, show that the maximum deflection occurs at x = √[(L2 - b2)/3].

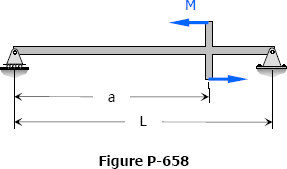
Solution to Problem 658 | Deflections in Simply Supported Beams
Problem 658
For the beam shown in Fig. P-658, find the value of EIδ at the point of application of the couple.