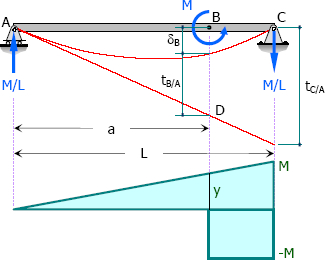
$\dfrac{y}{a} = \dfrac{M}{L}$
$y = Ma/L$
$EI \, t_{B/A} = (Area_{AB}) \, \bar{X}_B$
$EI \, t_{B/A} = \frac{1}{2}(ay)(\frac{1}{3}a)$
$EI \, t_{B/A} = \frac{1}{6}a^2(Ma/L)$
$EI \, t_{B/A} = \dfrac{Ma^3}{6L}$
$EI \, t_{C/A} = (Area_{AC}) \, \bar{X}_C$
$EI \, t_{C/A} = \frac{1}{2}(LM)(\frac{1}{3}L) - M(L - a) [ \, \frac{1}{2}(L - a) \, ]$
$EI \, t_{C/A} = \frac{1}{6}ML^2 - \frac{1}{2}M(L - a)^2$
By ratio and proportion:
$\dfrac{\delta_B + t_{B/A}}{a} = \dfrac{t_{C/A}}{L}$
$\delta_B = \dfrac{a}{L}t_{C/A} - t_{B/A}$
$EI \, \delta_B = \dfrac{a}{L}EI \, t_{C/A} - EI \, t_{B/A}$
$EI \, \delta_B = \dfrac{a}{L} [ \, \frac{1}{6}ML^2 - \frac{1}{2}M(L - a)^2 \, ] - \dfrac{Ma^3}{6L}$
$EI \, \delta_B = \dfrac{a}{L} [ \, \frac{1}{6}ML^2 - \frac{1}{2}M(L - a)^2 - \frac{1}{6}Ma^2 \, ]$
$EI \, \delta_B = \dfrac{Ma}{6L} [ \, L^2 - 3(L - a)^2 - a^2 \, ]$
$EI \, \delta_B = \dfrac{Ma}{6L} [ \, L^2 - 3(L^2 - 2La + a^2) - a^2 \, ]$
$EI \, \delta_B = \dfrac{Ma}{6L} [ \, L^2 - 3L^2 + 6La - 3a^2 - a^2 \, ]$
$EI \, \delta_B = \dfrac{Ma}{6L} [ \, -2L^2 + 6La - 4a^2 \, ]$
$EI \, \delta_B = -\dfrac{Ma}{3L} (L^2 - 3La + 2a^2)$
The negative sign indicates that the deflection is opposite to the direction sketched in the figure. Thus,
$EI \, \delta_B = \dfrac{Ma}{3L} (L^2 - 3La + 2a^2)$ upward answer
