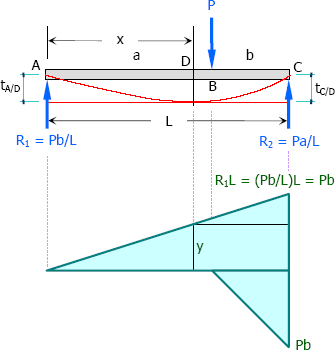
$\Sigma M_{R2} = 0$
$LR_1 = Pb$
$R_1 = Pb/L$
$\Sigma M_{R1} = 0$
$LR_2 = Pa$
$R_2 = Pa/L$
$\dfrac{y}{x} = \dfrac{Pb}{L}$
$y = \dfrac{Pb}{L}x$
$t_{A/D} = \dfrac{1}{EI}(Area_{AD}) \, \bar{X}_A$
$t_{A/D} = \dfrac{1}{EI}[ \, \frac{1}{2}xy (\frac{2}{3}x \, ]$
$t_{A/D} = \dfrac{1}{EI}[ \, \frac{1}{3}x^2y \, ]$
$t_{A/D} = \dfrac{1}{EI} \left[ \, \frac{1}{3}x^2 \left( \dfrac{Pb}{L}x \right) \right]$
$t_{A/D} = \dfrac{1}{EI} \dfrac{Pb}{3L}x^3$
$t_{C/D} = \dfrac{1}{EI}(Area_{CD}) \, \bar{X}_C$
$t_{C/D} = \dfrac{1}{EI} [ \, \frac{1}{6}(L - x)^2(Pb - y) + \frac{1}{2}(L - x)^2 y - \frac{1}{6}Pb^3 \, ]$
$t_{C/D} = \dfrac{1}{EI} \left[ \frac{1}{6}(L - x)^2 \left( Pb - \dfrac{Pb}{L}x \right) + \frac{1}{2}(L - x)^2 \left( \dfrac{Pb}{L}x \right) - \frac{1}{6}Pb^3 \right]$
$t_{C/D} = \dfrac{1}{EI} \left[ \frac{1}{6}Pb(L - x)^2 \left( 1 - \dfrac{x}{L} \right) + \frac{1}{2}Pb(L - x)^2 \left( \dfrac{x}{L} \right) - \frac{1}{6}Pb^3 \right]$
$t_{C/D} = \dfrac{1}{EI} \left[ \dfrac{Pb}{6L}(L - x)^3 + \dfrac{Pb}{2L}(L - x)^2x - \dfrac{Pb^3}{6} \right]$
From the figure:
$t_{A/D} = t_{C/D}$
$\dfrac{1}{EI} \dfrac{Pb}{3L}x^3 = \dfrac{1}{EI} \left[ \dfrac{Pb}{6L}(L - x)^3 + \dfrac{Pb}{2L}(L - x)^2x - \dfrac{Pb^3}{6} \right]$
$\dfrac{Pb}{3L}x^3 = \dfrac{Pb}{6L}(L - x)^3 + \dfrac{Pb}{2L}(L - x)^2x - \dfrac{Pb^3}{6}$
$\dfrac{2x^3}{L} = \dfrac{(L - x)^3}{L} + \dfrac{3(L - x)^2x}{L} - b^2$
$2x^3 = (L - x)^3 + 3(L - x)^2x - Lb^2$
$2x^3 = (L^3 - 3L^2x + 3Lx^2 - x^3) + 3(L^2 - 2Lx + x^2)x - Lb^2$
$2x^3 = L^3 - 3L^2x + 3Lx^2 - x^3 + 3L^2x - 6Lx^2 + 3x^3 - Lb^2$
$0 = L^3 - 3Lx^2 - Lb^2$
$0 = L^2 - 3x^2 - b^2$
$3x^2 = L^2 - b^2$
$x = \sqrt{\dfrac{L^2 - b^2}{3}}$ (okay!)
