Problem 813
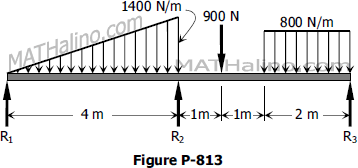
Determine the moment over the support R2 of the beam shown in Fig. P-813.
Problem 726
A beam of length L, perfectly restrained at both ends, supports a concentrated load P at midspan. Determine the end moment and maximum deflection.
Problem 656
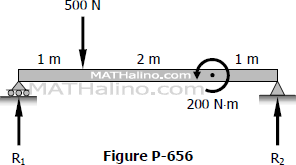
Find the value of EIδ at the point of application of the 200 N·m couple in Fig. P-656.
Problem 655
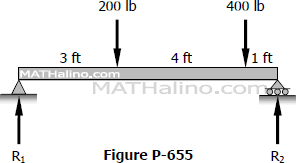
Find the value of EIδ under each concentrated load of the beam shown in Fig. P-655.
Problem 335
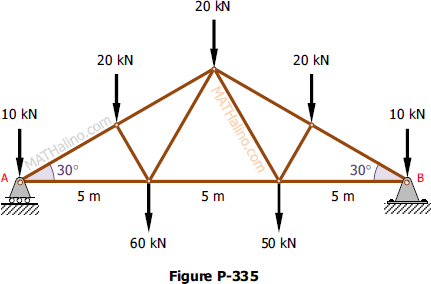
The roof truss in Fig. P-335 is supported by a roller at A and a hinge at B. Find the values of the reactions.
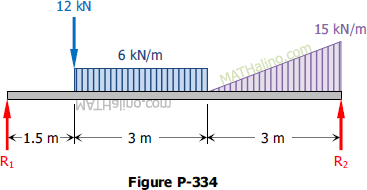
Problem 334
Determine the reactions for the beam loaded as shown in Fig. P-334.
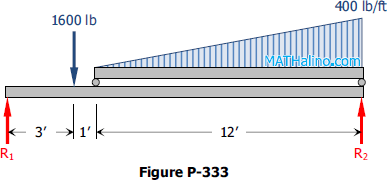
Problem 333
Determine the reactions R1 and R2 of the beam in Fig. P-333 loaded with a concentrated load of 1600 lb and a load varying from zero to an intensity of 400 lb per ft.
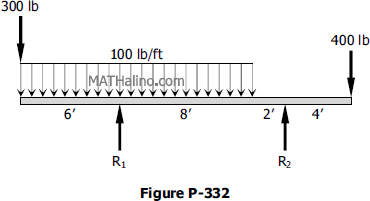
Problem 332
Determine the reactions for the beam shown in Fig. P-332.
Problem 690
The beam shown in Fig. P-690 has a rectangular cross section 50 mm wide. Determine the proper depth d of the beam if the midspan deflection of the beam is not to exceed 20 mm and the flexural stress is limited to 10 MPa. Use E = 10 GPa.
Problem 689
The beam shown in Fig. P-689 has a rectangular cross section 4 inches wide by 8 inches deep. Compute the value of P that will limit the midspan deflection to 0.5 inch. Use E = 1.5 × 106 psi.
