point load

Problem 687
Determine the midspan deflection of the beam shown in Fig. P-687 if E = 10 GPa and I = 20 × 10⁶ mm⁴.
 

Problem 680
Determine the midspan value of EIδ for the beam loaded as shown in Fig. P-680.
 

Problem 674
Find the deflection midway between the supports for the overhanging beam shown in Fig. P-674.
 

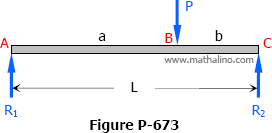
Problem 673
For the beam shown in Fig. P-673, show that the midspan deflection is δ = (Pb/48EI) (3L² - 4b²).
 

Problem 668
For the beam shown in Fig. P-668, compute the value of P that will cause the tangent to the elastic curve over support R₂ to be horizontal. What will then be the value of EIδ under the 100-lb load?
 

Problem 667
Determine the value of EIδ at the right end of the overhanging beam shown in Fig. P-667. Is the deflection up or down?
 

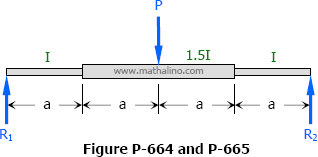
Problem 664
The middle half of the beam shown in Fig. P-664 has a moment of inertia 1.5 times that of the rest of the beam. Find the midspan deflection. (Hint: Convert the M diagram into an M/EI diagram.)
 

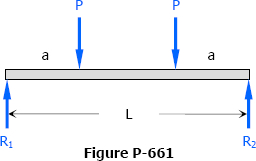
Problem 661
Compute the midspan deflection of the symmetrically loaded beam shown in Fig. P-661. Check your answer by letting a = L/2 and comparing with the answer to Problem 609.