point load

Problem 659
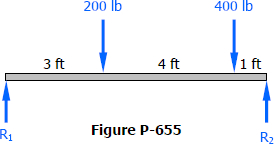
A simple beam supports a concentrated load placed anywhere on the span, as shown in Fig. P-659. Measuring x from A, show that the maximum deflection occurs at x = √[(L² - b²)/3].
 

Problem 655
Find the value of EIδ under each concentrated load of the beam shown in Fig. P-655.
 

Problem 641
For the cantilever beam shown in Fig. P-641, what will cause zero deflection at A?
 

Problem 640
Compute the value of δ at the concentrated load in Prob. 639. Is the deflection upward downward?
 

Problem 636
The cantilever beam shown in Fig. P-636 has a rectangular cross-section 50 mm wide by h mm high. Find the height h if the maximum deflection is not to exceed 10 mm. Use E = 10 GPa.
 

Problem 632
For the beam loaded as shown in Fig. P-632, compute the value of (Area_AB) barred(X)_A. From this result, is the tangent drawn to the elastic curve at B directed up or down to the right? (Hint: Refer to the deviation equations and rules of sign.)
 

Problem 630
For the beam loaded as shown in Fig. P-630, compute the value of (Area_AB)barred(X)_A . From the result determine whether the tangent drawn to the elastic curve at B slopes up or down to the right. (Hint: Refer to the deviation equations and rules of sign.)
 

Problem 625
For the beam loaded as shown in Fig. P-625, compute the moment of area of the M diagrams between the reactions about both the left and the right reaction. (Hint: Draw the moment diagram by parts from right to left.)
 

Problem 624
For the beam loaded as shown in Fig. P-624, compute the moment of area of the M diagrams between the reactions about both the left and the right reaction.