maximum deflection

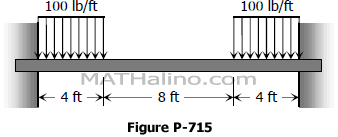
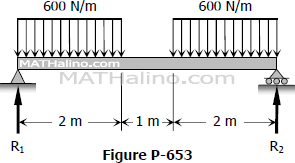
Example 01: Maximum bending stress, shear stress, and deflection

Problem
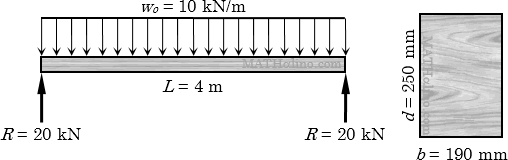
A timber beam 4 m long is simply supported at both ends. It carries a uniform load of 10 kN/m including its own weight. The wooden section has a width of 200 mm and a depth of 260 mm and is made up of 80% grade Apitong. Use dressed dimension by reducing its dimensions by 10 mm.

Properties of Apitong
Bending and tension parallel to grain = 16.5 MPa
Shear parallel to grain = 1.73 MPa
Modulus of elasticity in bending = 7.31 GPa

What is the maximum flexural stress of the beam?
What is the maximum shearing stress of the beam?
What is the maximum deflection of the beam?

Problem 730 | Uniform loads at each end of fully restrained beam

Problem 703
Determine the end moment and maximum deflection for a perfectly restrained beam loaded as shown in Fig. P-730.

Problem 729 | Uniform load over the center part of fixed-ended beam

Problem 728 | Isosceles triangular load over the entire span of fully restrained beam

Problem 728
Determine the end moment and maximum deflection of a perfectly restrained beam loaded as shown in Fig. P-728.

Problem 727 | Fully restrained beam with uniform load over the entire span

Problem 727
Repeat Problem 726 assuming that the concentrated load is replaced by a uniformly distributed load of intensity w_o over the entire length.

Problem 726 | Fully restrained beam with concentrated load at midspan

Problem 726
A beam of length L, perfectly restrained at both ends, supports a concentrated load P at midspan. Determine the end moment and maximum deflection.

Problem 715 | Distributed loads placed symmetrically over fully restrained beam

Problem 12
Determine the moment and maximum EIδ for the restrained beam shown in Fig. RB-012. (Hint: Let the redundants be the shear and moment at the midspan. Also note that the midspan shear is zero.)

Problem 653 | Beam Deflection by Conjugate Beam Method

Problem 653
Compute the midspan value of EIδ for the beam shown in Fig. P-653. (Hint: Draw the M diagram by parts, starting from midspan toward the ends. Also take advantage of symmetry.

Read more about Problem 653 | Beam Deflection by Conjugate Beam Method
Add new comment
80725 reads

Method of Superposition | Beam Deflection

The slope or deflection at any point on the beam is equal to the resultant of the slopes or deflections at that point caused by each of the load acting separately.

Read more about Method of Superposition | Beam Deflection
Add new comment
201651 reads

Midspan Deflection | Deflections in Simply Supported Beams

In simply supported beams, the tangent drawn to the elastic curve at the point of maximum deflection is horizontal and parallel to the unloaded beam. It simply means that the deviation from unsettling supports to the horizontal tangent is equal to the maximum deflection. If the simple beam is symmetrically loaded, the maximum deflection will occur at the midspan.