maximum deflection

Problem 665
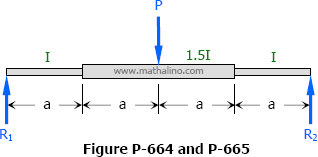
Replace the concentrated load in Prob. 664 by a uniformly distributed load of intensity w_o acting over the middle half of the beam. Find the maximum deflection.
 

Problem 664
The middle half of the beam shown in Fig. P-664 has a moment of inertia 1.5 times that of the rest of the beam. Find the midspan deflection. (Hint: Convert the M diagram into an M/EI diagram.)
 

Problem 663
Determine the maximum deflection of the beam carrying a uniformly distributed load over the middle portion, as shown in Fig. P-663. Check your answer by letting 2b = L.
 

Problem 662
Determine the maximum deflection of the beam shown in Fig. P-662. Check your result by letting a = L/2 and comparing with case 8 in Table 6-2. Also, use your result to check the answer to Prob. 653.
 

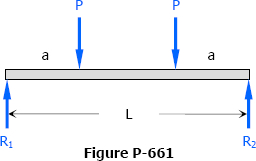
Problem 661
Compute the midspan deflection of the symmetrically loaded beam shown in Fig. P-661. Check your answer by letting a = L/2 and comparing with the answer to Problem 609.
 

Problem 660
A simply supported beam is loaded by a couple M at its right end, as shown in Fig. P-660. Show that the maximum deflection occurs at x = 0.577L.
 

Problem 659
A simple beam supports a concentrated load placed anywhere on the span, as shown in Fig. P-659. Measuring x from A, show that the maximum deflection occurs at x = √[(L² - b²)/3].
 

Problem 653
Compute the midspan value of EIδ for the beam shown in Fig. P-653. (Hint: Draw the M diagram by parts, starting from midspan toward the ends. Also take advantage of symmetry to note that the tangent drawn to the elastic curve at midspan is horizontal.)
 

Problem 647
Find the maximum value of EIδ for the beam shown in Fig. P-647.
 

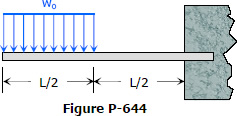
Problem 644
Determine the maximum deflection for the beam loaded as shown in Fig. P-644.