maximum deflection

Problem 643
Find the maximum value of EIδ for the cantilever beam shown in Fig. P-643.
 

Problem 642
Find the maximum deflection for the cantilever beam loaded as shown in Figure P-642 if the cross section is 50 mm wide by 150 mm high. Use E = 69 GPa.
 

Problem 636
The cantilever beam shown in Fig. P-636 has a rectangular cross-section 50 mm wide by h mm high. Find the height h if the maximum deflection is not to exceed 10 mm. Use E = 10 GPa.
 

Problem 621
Determine the value of EIδ midway between the supports for the beam shown in Fig. P-621. Check your result by letting a = 0 and comparing with Prob. 606. (Apply the hint given in Prob. 620.)
 

Problem 620
Find the midspan deflection δ for the beam shown in Fig. P-620, carrying two triangularly distributed loads. (Hint: For convenience, select the origin of the axes at the midspan position of the elastic curve.)
 

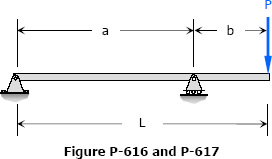
Problem 616
For the beam loaded as shown in Fig. P-616, determine (a) the deflection and slope under the load P and (b) the maximum deflection between the supports.
 

Problem 610
The simply supported beam shown in Fig. P-610 carries a uniform load of intensity w_o symmetrically distributed over part of its length. Determine the maximum deflection δ and check your result by letting a = 0 and comparing with the answer to Problem 606.
 

Problem 609
As shown in Fig. P-609, a simply supported beam carries two symmetrically placed concentrated loads. Compute the maximum deflection δ.
 

Problem 607
Determine the maximum value of EIy for the cantilever beam loaded as shown in Fig. P-607. Take the origin at the wall.
 

Problem 606
Determine the maximum deflection δ in a simply supported beam of length L carrying a uniformly distributed load of intensity w_o applied over its entire length.