Problem 910
A timber beam AD, 6 in. thick by 10 in. high and loaded as shown in Figure P-910, is pinned at its lower end and supported by a horizontal cable CE. Compute the maximum compressive stress developed in the beam.
Problem 1008
A timber beam 150 mm wide by 250 mm deep is to be reinforced at the top and bottom by steel plates 10 mm thick. How wide should the steel plates be if the beam is to resist a moment of 40 kN·m? Assume that n = 15 and the allowable stresses in the wood and steel are 10 MPa and 120 MPa, respectively.
Problem 1007
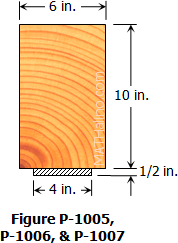
A uniformly distributed load of 300 lb/ft (including the weight of the beam) is simply supported on a 20-ft span. The cross section of the beam is described in Problem 1005. If n = 20, determine the maximum stresses produced in the wood and the steel.
Problem 1006
Determine the width b of the 1/2-in. steel plate fastened to the bottom of the beam in Problem 1005 that will simultaneously stress the wood and the steel to their permissible limits of 1200 psi and 18 ksi, respectively.
Problem 1005
A timber beam 6 in. by 10 in. is reinforced only at the bottom by a steel plate as shown in Fig. P-1005. Determine the concentrated load that can be applied at the center of a simply supported span 18 ft long if n = 20, fs ≤ 18 ksi and fw ≤ 1200 psi. Show that the neutral axis is 7.1 in. below the top and that INA = 1160 in.4.
Problem 4
The stiffness of a rectangular beam is proportional to the breadth and the cube of the depth. Find the shape of the stiffest beam that can be cut from a log of a given size.
Problem 581
A laminated beam is composed of five planks, each 6 in. by 2 in., glued together to form a section 6 in. wide by 10 in. high. The allowable shear stress in the glue is 90 psi, the allowable shear stress in the wood is 120 psi, and the allowable flexural stress in the wood is 1200 psi. Determine the maximum uniformly distributed load that can be carried by the beam on a 6-ft simple span.
