rectangular beam

Example 04: Required Depth of Rectangular Timber Beam Based on Allowable Bending, Shear, and Deflection

Problem
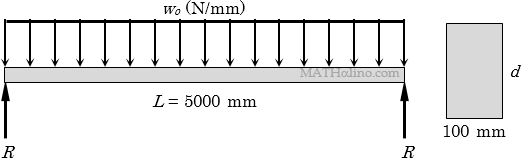
A beam 100 mm wide is to be loaded with 3 kN concentrated loads spaced uniformly at 0.40 m on centers throughout the 5 m span. The following data are given:

Allowable bending stress = 24 MPa
Allowable shear stress = 1.24 MPa
Allowable deflection = 1/240 of span
Modulus of elasticity = 18,600 MPa
Weight of wood = 8 kN/m3
  1. Find the depth d considering bending stress only.
  2. Determine the depth d considering shear stress only.
  3. Calculate the depth d considering deflection only.

 

beam-003-required-depth.gif

 

Example 01: Maximum bending stress, shear stress, and deflection

Problem
A timber beam 4 m long is simply supported at both ends. It carries a uniform load of 10 kN/m including its own weight. The wooden section has a width of 200 mm and a depth of 260 mm and is made up of 80% grade Apitong. Use dressed dimension by reducing its dimensions by 10 mm.

Properties of Apitong
Bending and tension parallel to grain = 16.5 MPa
Shear parallel to grain = 1.73 MPa
Modulus of elasticity in bending = 7.31 GPa
  1. What is the maximum flexural stress of the beam?
  2. What is the maximum shearing stress of the beam?
  3. What is the maximum deflection of the beam?

 

2006-may-ce-board-stresses-in-timber-beam.gif

 

Bending Stress and Shearing Stress in Timber Beam

Bending Stress
$f_b = \dfrac{M}{S} = \dfrac{Mc}{I}$
 

Horizontal Shear Stress
$f_v = \dfrac{VQ}{Ib}$

 bending-member-corss-section-any-shape.gif
For Rectangular Sections
$f_b = \dfrac{6M}{bd^2}$
 

$f_v = \dfrac{3V}{2bd}$

Example 02: Moment Capacity of a Concrete Beam

Problem
A reinforced concrete beam 300 mm wide has an effective depth of 600 mm. It is reinforced with 4-32 mm diameter bars for tension. f’c = 21 MPa and fy = 275 MPa. Find the moment capacity of the beam.
 

wsd-example-02-moment-capacity-beam.jpg

 

Example 01: Required Steel Area of Reinforced Concrete Beam

Problem
A rectangular concrete beam is reinforced in tension only. The width is 300 mm and the effective depth is 600 mm. The beam carries a moment of 80 kN·m which causes a stress of 5 MPa in the extreme compression fiber of concrete. Use n = 9.
1.   What is the distance of the neutral axis from the top of the beam?
2.   Calculate the required area for steel reinforcement.
3.   Find the stress developed in the steel.
 

wsd-example-01-unknown-steel-area.jpg

 

Solution to Problem 690 | Beam Deflection by Method of Superposition

Problem 690
The beam shown in Fig. P-690 has a rectangular cross section 50 mm wide. Determine the proper depth d of the beam if the midspan deflection of the beam is not to exceed 20 mm and the flexural stress is limited to 10 MPa. Use E = 10 GPa.
 

Solution to Problem 642 | Deflection of Cantilever Beams

Problem 642
Find the maximum deflection for the cantilever beam loaded as shown in Figure P-642 if the cross section is 50 mm wide by 150 mm high. Use E = 69 GPa.
 

Uniform load over the free end of cantilever beam

 

Solution to Problem 583 | Design for Flexure and Shear

Problem 583
A rectangular beam 6 in. wide by 10 in. high supports a total distributed load of W and a concentrated load of 2W applied as shown in Fig. P-583. If fb ≤ 1500 psi and fv ≤ 120 psi, determine the maximum value of W.
 

Solution to Problem 571 | Horizontal Shearing Stress

Problem 571
For a beam with the same cross section as that in Prob. 570, plot the shearing stress distribution across the section at a section where the shearing force is V = 1800 lb.
 

Solution to Problem 570 | Horizontal Shearing Stress

Problem 570
A uniformly distributed load of 200 lb/ft is carried on a simply supported beam span. If the cross-section is as shown in Fig. P-570, determine the maximum length of the beam if the shearing stress is limited to 80 psi. Assume the load acts over the entire length of the beam.
 

Pages

Subscribe to RSS - rectangular beam