Beam Deflection

Problem 666
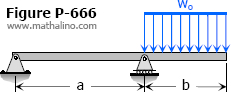
Determine the value of EIδ at the right end of the overhanging beam shown in Fig. P-666.
 

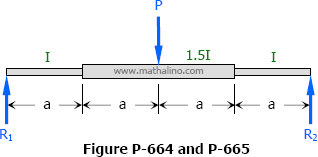
Problem 665
Replace the concentrated load in Prob. 664 by a uniformly distributed load of intensity w_o acting over the middle half of the beam. Find the maximum deflection.
 

Problem 664
The middle half of the beam shown in Fig. P-664 has a moment of inertia 1.5 times that of the rest of the beam. Find the midspan deflection. (Hint: Convert the M diagram into an M/EI diagram.)
 

Problem 663
Determine the maximum deflection of the beam carrying a uniformly distributed load over the middle portion, as shown in Fig. P-663. Check your answer by letting 2b = L.
 

Problem 662
Determine the maximum deflection of the beam shown in Fig. P-662. Check your result by letting a = L/2 and comparing with case 8 in Table 6-2. Also, use your result to check the answer to Prob. 653.
 

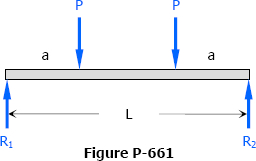
Problem 661
Compute the midspan deflection of the symmetrically loaded beam shown in Fig. P-661. Check your answer by letting a = L/2 and comparing with the answer to Problem 609.
 

Problem 660
A simply supported beam is loaded by a couple M at its right end, as shown in Fig. P-660. Show that the maximum deflection occurs at x = 0.577L.
 

Problem 659
A simple beam supports a concentrated load placed anywhere on the span, as shown in Fig. P-659. Measuring x from A, show that the maximum deflection occurs at x = √[(L² - b²)/3].
 

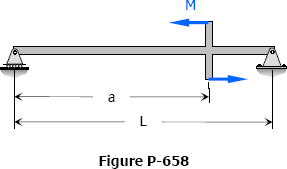
Problem 658
For the beam shown in Fig. P-658, find the value of EIδ at the point of application of the couple.
 

Problem 657
Determine the midspan value of EIδ for the beam shown in Fig. P-657.