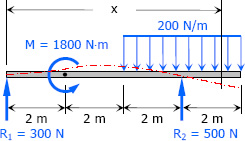
$\Sigma M_{R2} = 0$
$6R_1 + 200(4)(0) = 1800$
$R_1 = 300 \, \text{N}$
$\Sigma M_{R1} = 0$
$6R_2 + 1800 = 200(4)(6)$
$R_2 = 500 \, \text{N}$
$EI \, y'' = 300x - 1800 \, \langle \, x - 2 \, \rangle^0 + 500 \, \langle \, x - 6 \, \rangle - \frac{1}{2} (200) \, \langle \, x - 4 \rangle^2$
$EI \, y'' = 300x - 1800 \, \langle \, x - 2 \, \rangle^0 + 500 \, \langle \, x - 6 \, \rangle - 100 \, \langle \, x - 4 \rangle^2$
$EI \, y' = 150x^2 - 1800 \, \langle \, x - 2 \, \rangle + 250 \, \langle \, x - 6 \, \rangle^2 - \frac{100}{3} \, \langle \, x - 4 \rangle^3 + C_1$
$EI \, y = 50x^3 - 900 \, \langle \, x - 2 \, \rangle^2 + \frac{250}{3} \, \langle \, x - 6 \, \rangle^3 - \frac{25}{3} \, \langle \, x - 4 \rangle^4 + C_1x + C_2$
At x = 0, y = 0, therefore C2 = 0
At x = 6 m, y = 0
0 = 50(63) - 900(42) - (25/3)(24) + 6C1
C1 = 5600/9 N·m3
Therefore,
$EI \, y = 50x^3 - 900 \, \langle \, x - 2 \, \rangle^2 + \frac{250}{3} \, \langle \, x - 6 \, \rangle^3 - \frac{25}{3} \, \langle \, x - 4 \rangle^4 + \frac{5600}{9}x$
At x = 3 m
$EI \, y = 50(3^3) - 900(1^2) + \frac{5600}{9}(3)$
$EI \, y = \frac{6950}{3} \, \text{N}\cdot\text{m}^3$ answer
