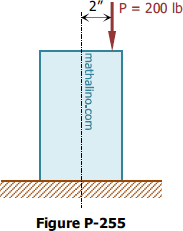
Problem 527 and Problem 528 | Friction
Problem 527
A homogeneous cylinder 3 m in diameter and weighing 30 kN is resting on two inclined planes as shown in Fig. P-527. If the angle of friction is 15° for all contact surfaces, compute the magnitude of the couple required to start the cylinder rotating counterclockwise.

Problem 528
Instead of a couple, determine the minimum horizontal force P applied tangentially to the left at the top of the cylinder described in Prob. 527 to start the cylinder rotating counterclockwise.