$M_1L_1 + 2M_2(L_1 + L_2) + M_3L_2 + \dfrac{6A_1\bar{a}_1}{L_1} + \dfrac{6A_2\bar{b}_2}{L_2} = 0$
Where
$L_1 = L_2 = L$
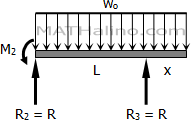
$M_1 = M_3 = -w_ox(\frac{1}{2}x) = -\frac{1}{2}w_ox^2$
$\dfrac{6A_1\bar{a}_1}{L_1} = \dfrac{6A_2\bar{b}_2}{L_2} = \frac{1}{4}w_oL^3$
Thus,
$-\frac{1}{2}w_ox^2 (L) + 2M_2(L + L) - \frac{1}{2}w_ox^2 (L) + \frac{1}{4}w_oL^3 + \frac{1}{4}w_oL^3 = 0$
$4L\,M_2 - w_ox^2 L + \frac{1}{2}w_oL^3 = 0$
$M_2 = \frac{1}{4}w_ox^2 - \frac{1}{8}w_oL^2$
 $\Sigma F_V = 0$
$\Sigma F_V = 0$
$3R = w_o (2L + 2x)$
$R = \frac{2}{3}w_o(L + x)$
$M_2 = \Sigma M_{\text{to the right of }R_2}$
$M_2 = RL - w_o(L+ x)[ \, \frac{1}{2}(L + x) \, ]$
$\frac{1}{4}w_ox^2 - \frac{1}{8}w_oL^2 = \frac{2}{3}w_o(L + x)L - \frac{1}{2}w_o(L + x)^2$
$\frac{1}{4}w_ox^2 - \frac{1}{8}w_oL^2 = \frac{2}{3}w_o(L + x)L - \frac{1}{2}w_o(L^2 + 2Lx + x^2)$
$\frac{1}{4}w_ox^2 - \frac{1}{8}w_oL^2 = \frac{2}{3}w_oL^2 + \frac{2}{3}w_oLx - \frac{1}{2}w_oL^2 - w_oLx - \frac{1}{2}w_ox^2$
$\frac{3}{4}w_ox^2 + + \frac{1}{3}w_oLx - \frac{7}{24}w_oL^2 = 0$
$18x^2 + 8L\,x - 7L^2 = 0$
$x = \dfrac{-8L \pm \sqrt{(8L)^2 - 4(18)(-7L^2)}}{2(18)} = \dfrac{-8L \pm \sqrt{64L^2 + 504L^2}}{36}$
$x = \dfrac{-8L \pm 2\sqrt{142}\,L}{36} = \frac{-4-\sqrt{142}}{18}L ~ \text{and} ~ \frac{-4+\sqrt{142}}{18}L$
Use,
$x = \frac{-4+\sqrt{142}}{18}L = 0.4398L$ answer
