Problem 706 | Solution of Propped Beam with Decreasing Load

Tags:

Example 03
The propped beam shown in Fig. P -706 is loaded by decreasing triangular load varying from w_o from the simple end to zero at the fixed end. Find the support reactions and sketch the shear and moment diagrams

Propped with decreasing load from w at simple support to zero at the fixed end.

Solution by Double Integration Method

Click here to show or hide the solution

By ratio and proportion:
$\dfrac{y}{L - x} = \dfrac{w_o}{L}$

$y = \dfrac{w_o}{L}(L - x)$

Magnitude of load at any point on the decreasing load of propped beam.

Solving for moment equation
$M = R_Ax - \frac{1}{2}(x)(w_o)(\frac{2}{3}x) - \frac{1}{2}(x)(y)(\frac{1}{3}x)$

$M = R_Ax - \frac{1}{3}w_ox^2 - \frac{1}{6}x^2y$

$M = R_Ax - \frac{1}{3}w_ox^2 - \frac{1}{6}x^2 \left[ \dfrac{w_o}{L}(L - x) \right]$

$M = R_Ax - \dfrac{w_o}{3}x^2 - \dfrac{w_o}{6L}(Lx^2 - x^3)$

Doing the double integration
$EI \, y'' = R_Ax - \dfrac{w_o}{3}x^2 - \dfrac{w_o}{6L}(Lx^2 - x^3)$

$EI \, y' = \dfrac{R_A}{2}x^2 - \dfrac{w_o}{9}x^3 - \dfrac{w_o}{6L} \left( \dfrac{Lx^3}{3} - \dfrac{x^4}{4} \right) + C_1$

$EI \, y = \dfrac{R_A}{6}x^3 - \dfrac{w_o}{36}x^4 - \dfrac{w_o}{6L} \left( \dfrac{Lx^4}{12} - \dfrac{x^5}{20} \right) + C_1x + C_2$

Boundary conditions
At x = 0, y = 0, C₂ = 0

At x = L, y = 0
$0 = \dfrac{R_AL^3}{6} - \dfrac{w_oL^4}{36} - \dfrac{w_o}{6L} \left( \dfrac{L^4}{12} - \dfrac{L^4}{20} \right) + C_1L + 0$

$0 = \dfrac{R_AL^3}{6} - \dfrac{w_oL^4}{36} - \dfrac{w_oL^4}{180} + C_1L$

$C_1 = \dfrac{w_oL^3}{30} - \dfrac{R_AL^2}{6}$

At x = L, y' = 0
$0 = \dfrac{R_AL^2}{2} - \dfrac{w_oL^3}{9} - \dfrac{w_o}{6L} \left( \dfrac{L^4}{3} - \dfrac{L^4}{4} \right) + \left( \dfrac{w_oL^3}{30} - \dfrac{R_AL^2}{6} \right)$

$0 = \dfrac{R_AL^2}{2} - \dfrac{w_oL^3}{9} - \dfrac{w_oL^3}{72} + \dfrac{w_oL^3}{30} - \dfrac{R_AL^2}{6}$

$\dfrac{R_AL^2}{3} = \dfrac{11w_oL^3}{120}$

$R_A = \dfrac{11w_oL}{40}$ answer

Solution by Superposition Method

Click here to show or hide the solution

Resolution of forces for method of superposition

Decreasing triangular load is not listed in the summary of beam loadings. It is therefore necessary to resolve this load into loads that are in the list. In this case, the load was resolved into uniformly distributed load and upward triangular load as shown. The sum of such loads is equal to the one that is given in the problem.

From the figure, it is clear that

$\delta_1 + \delta_3 = \delta_2$

$\dfrac{R_AL^3}{3EI} + \dfrac{w_oL^4}{30EI} = \dfrac{w_oL^4}{8EI}$

$\dfrac{R_A}{3} + \dfrac{w_oL}{30} = \dfrac{w_oL}{8}$

$\dfrac{R_A}{3} = \dfrac{11w_oL}{120}$

$R_A = \dfrac{11w_oL}{40}$ answer

Superposition Method Using Point Load and Integration

Click here to show or hide the solution

Another way of solving the reaction at A is by the use of derivative. From Case No. 2, the deflection at the free end of cantilever beam is

$\delta = \dfrac{Pa^2}{6EI}(3L - a)$

For this problem $P = y \, dx$ , $a = L - x$ , and $\delta = d \delta_2$ .

$d\delta_2 = \dfrac{y\,dx(L-x)^2}{6EI}[ \, 3L - (L - x) \, ]$

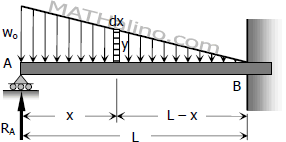From the figure,
$\dfrac{y}{L - x} = \dfrac{w_o}{L}$

$y = \dfrac{w_o}{L}(L - x)$

Thus,
$d\delta_2 = \dfrac{\left[ \dfrac{w_o}{L}(L - x) \right](L - x)^2}{6EI}[ \, 3L - (L - x) \, ] \, dx$

$d\delta_2 = \dfrac{w_o(L - x)^3}{6L \, EI}[ \, 3L - (L - x) \, ] \, dx$

$d\delta_2 = \dfrac{w_o}{2EI}(L - x)^3 \, dx - \dfrac{w_o}{6L \, EI}(L - x)^4 \, dx$

$\displaystyle \delta_2 = \dfrac{w_o}{2EI} \int_0^L (L - x)^3 \, dx - \dfrac{w_o}{6L \, EI} \int_0^L (L - x)^4 \, dx$

$\delta_1$ = end deflection due to R_A

$\delta_1 = \dfrac{R_AL^3}{3EI}$

$\delta_1 = \delta_2$

$\displaystyle \dfrac{R_AL^3}{3EI} = \dfrac{w_o}{2EI} \int_0^L (L - x)^3 \, dx - \dfrac{w_o}{6L \, EI} \int_0^L (L - x)^4 \, dx$

$\displaystyle R_A = \dfrac{3w_o}{2L^3} \int_0^L (L - x)^3 \, dx - \dfrac{w_o}{2L^4} \int_0^L (L - x)^4 \, dx$

$R_A = \dfrac{3w_o}{2L^3} \left[ -\dfrac{(L - x)^4}{4} \right] - \dfrac{w_o}{2L^4} \left[ -\dfrac{(L - x)^5}{5} \right]$

$R_A = -\dfrac{3w_o}{8L^3} \left[ 0^4 - L^4 \right] + \dfrac{w_o}{10L^4} \left[ 0^5 - L^5 \right]$

$R_A = \dfrac{3w_oL}{8} - \dfrac{w_oL}{10}$

$R_A = \dfrac{11w_oL}{40}$ answer

Shear and Moment Diagrams

Click here to show or hide the solution

The reaction at the simple support R_A was solved using two different methods above.
$R_A = \dfrac{11w_oL}{40}$ answer

Solving for vertical reaction at B
$\Sigma F_V = 0$

$R_A + R_B = \frac{1}{2}w_oL$

$\dfrac{11w_oL}{40} + R_B = \dfrac{w_oL}{2}$

$R_B = \dfrac{9w_oL}{40}$ answer

Solving for moment reaction at B
$M_B = R_AL – \frac{1}{2}w_oL(\frac{2}{3}L)$

$M_B = \left( \dfrac{9w_oL}{40} \right)L – \dfrac{w_oL^2}{3}$

$M_B = \dfrac{9w_oL^2}{40} – \dfrac{w_oL^2}{3}$

$M_B = –\dfrac{7w_oL^2}{120}$ answer

To Draw the Shear Diagram

The shear at A is equal to R_A
The load at AB is increasing from -w_o at A to zero at B, thus, the slope of shear diagram from A to B is also increasing from -w_o at A to zero at B.
The load between AB is 1st degree (linear), thus, the shear diagram between AB is 2nd degree (parabolic) with vertex at B and open upward.
The magnitude of shear at B is equal to -R_B. It is equal to the shear at A minus the triangular load between AB. See the magnitude of R_B above.
The shear diagram from A to B will become zero somewhere along AB, the point is denoted by C in the figure. To locate point C, two solutions are presented below.

Location of C, the point of zero shear
Point C is the location of zero shear which may also be the location of maximum moment.

By squared property of parabola
$\dfrac{(L - x_C)^2}{R_B} = \dfrac{L^2}{R_A + R_B}$
$(L - x_C)^2 = \dfrac{R_BL^2}{R_A + R_B}$

$(L - x_C)^2 = \dfrac{(\frac{9}{40}w_oL)L^2}{\frac{11}{40}w_oL + \frac{9}{40}w_oL}$

$(L - x_C)^2 = \dfrac{\frac{9}{40}w_oL^3}{\frac{1}{2}w_oL}$

$(L - x_C)^2 = \frac{9}{20}L^2$

$L - x_C = \pm \frac{3}{\sqrt{20}}L$

$x_C = \left(1 \pm \dfrac{3}{\sqrt{20}} \right)L$

$x_C = 1.6708L$ (absurd)
$x_C = 0.3292L$ answer

By shear equation
Another method of solving for x_C is to pass an exploratory section anywhere on AB and sum up all the vertical forces to the left of the exploratory section. The location of x_C is where the sum of all vertical forces equate to zero. Consider the figure shown to the right. Note that this figure is the same figure we used to find the reaction R_A by double integration method shown above. The double integration method shows the relationship of x and y which is $y = \dfrac{w_o}{L}(L - x)$ .

Sum of all vertical forces
$\Sigma F_V = R_A - \frac{1}{2}w_ox - \frac{1}{2}xy$

$\Sigma F_V = \dfrac{11w_oL}{40} - \dfrac{w_ox}{2} - \dfrac{w_ox}{2L}(L - x)$

$\Sigma F_V = \dfrac{11w_oL}{40} - \dfrac{w_ox}{2} - \dfrac{w_ox}{2} + \dfrac{w_ox^2}{2L}$

$\Sigma F_V = \dfrac{11w_oL}{40} - w_ox + \dfrac{w_ox^2}{2L}$

At point C, ΣF_V = 0 and x = x_C
$0 = \dfrac{11w_oL}{40} - w_ox_C + \dfrac{w_o{x_C}^2}{2L}$

$0 = \dfrac{11L}{40} - x_C + \dfrac{{x_C}^2}{2L}$

$0 = \frac{11}{20}L^2 - 2Lx_C + {x_C}^2$

${x_C}^2 - 2Lx_C = -\frac{11}{20}L^2$

${x_C}^2 - 2Lx_C + L^2= -\frac{11}{20}L^2 + L^2$

$(x_C - L)^2= \frac{9}{20}L^2$

$x_C - L= \pm \frac{3}{\sqrt{20}}L$

$x_C = \left(1 \pm \dfrac{3}{\sqrt{20}} \right)L$

$x_C = 1.6708L$ (absurd)
$x_C = 0.3292L$ answer

To Draw the Moment Diagram

The moment at simple support A is zero.
The shear diagram of AB is 2^nd degree curve, thus, the moment diagram between AB is 3^rd degree curve.
The moment at C can be computed in two ways; (a) by solving the area of shear diagram between A and C, and (b) by using the moment equation. For method (a), see the following links for similar situation of solving a partial area of parabolic spandrel.
- Simple beam with triangular load
- Simple beam with rectangular and trapezoidal loads
The solution below is using the approach mentioned in (b). From double integration method of solving R_A, the moment equation is given by

$M = R_Ax - \dfrac{w_o}{3}x^2 - \dfrac{w_o}{6L}(Lx^2 - x^3)$

$M = \dfrac{11w_oL}{40}x - \dfrac{w_o}{3}x^2 - \dfrac{w_o}{6L}(Lx^2 - x^3)$

For x = x_C = 0.3292L, M = M_C

$M_C = \dfrac{11w_oL}{40}(0.3292L) - \dfrac{w_o}{3}(0.3292L)^2 - \dfrac{w_o}{6L}[ \, L(0.3292L)^2 - (0.3292L)^3 \, ]$

$M_C = 0.0423w_oL^2$
In the same manner of solving for M_C, M_B can be found by using x = L. Thus,
$M_B = \dfrac{11w_oL^2}{40} - \dfrac{w_oL^2}{3} - \dfrac{w_o}{6L}(L^3 - L^3)$

$M_B = -\dfrac{7w_oL^2}{120}$ which confirms the solution above for M_B.
To locate the point of zero moment denoted by D in the figure, we will again use the moment equation; now with M = 0 and x = x_D.
$0 = \dfrac{11w_oL}{40}x_D - \dfrac{w_o}{3}{x_D}^2 - \dfrac{w_o}{6L}(L{x_D}^2 - {x_D}^3)$

$0 = \frac{11}{40}L - \dfrac{1}{3}x_D - \dfrac{x_D}{6L}(L - x_D)$

$0 = \frac{33}{20}L^2 - 2Lx_D - x_D(L - x_D)$

$0 = \frac{33}{20}L^2 - 3Lx_D + {x_D}^2$

${x_D}^2 - 3Lx_D = -\frac{33}{20}L^2$

${x_D}^2 - 3Lx_D + \frac{9}{4}L^2 = -\frac{33}{20}L^2 + \frac{9}{4}L^2$

$(x_D - \frac{3}{2}L)^2 = \frac{3}{5}L^2$

$x_D - \frac{3}{2}L = \pm \frac{3}{5}L$

$x_D = \left( \frac{3}{2} \pm \frac{3}{5} \right)L$

$x_D = 2.2746L$ (absurd)
$x_D = 0.7254L$ answer