$\Sigma M_{R2} = 0$
$LR_1 = \frac{1}{3}L \,(\frac{1}{2}Lw_o)$
$R_1 = \frac{1}{6}Lw_o$
$\Sigma M_{R1} = 0$
$LR_2 = \frac{2}{3}L \, (\frac{1}{2}Lw_o)$
$R_2 = \frac{1}{3}Lw_o$
To draw the Shear Diagram
- VA = R1 = 1/6 Lwo
- VB = VA + Area in load diagram
VB = 1/6 Lwo - 1/2 Lwo
VB = -1/3 Lwo
- Location of zero shear C:
By squared property of parabola:
x2 / (1/6 Lwo) = L2 / (1/6 Lwo + 1/3 Lwo)
6x2 = 2L2
x = L / √3
- The shear in AB is a parabola with vertex at A, the starting point of uniformly varying load. The load in AB is 0 at A to downward wo or -wo at B, thus the slope of shear diagram is decreasing. For decreasing slope, the parabola is open downward.
To draw the Moment Diagram
- MA = 0
- MC = MA + Area in shear diagram
MC = 0 + 2/3 (L/√3)(1/6 Lwo)
MC = 0.06415L2wo = Mmax
- MB = MC + Area in shear diagram
MB = MC - A1 (see figure for solving A1)
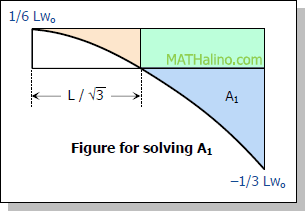
For A1:
A1 = 1/3 L(1/6 Lwo + 1/3 Lwo) - 1/3 (L/√3)(1/6 Lwo) - 1/6 Lwo (L - L/√3)
A1 = 0.16667L2wo - 0.03208L2wo - 0.07044L2wo
A1 = 0.06415L2wo
MB = 0.06415L2wo - 0.06415L2wo = 0
- The shear diagram is second degree curve, thus the moment diagram is a third degree curve. The maximum moment (highest point) occurred at C, the location of zero shear. The value of shears in AC is positive then the moment in AC is increasing; at CB the shear is negative, then the moment in CB is decreasing.
