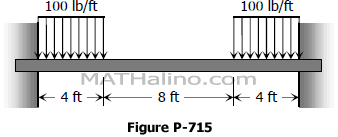
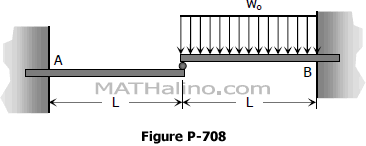
Problem 715 | Distributed loads placed symmetrically over fully restrained beam
Problem 12
Determine the moment and maximum EIδ for the restrained beam shown in Fig. RB-012. (Hint: Let the redundants be the shear and moment at the midspan. Also note that the midspan shear is zero.)