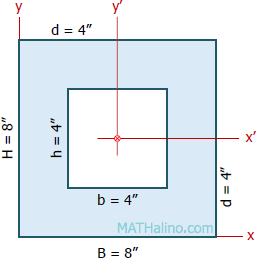
Centroidal moment of inertia
$\bar{I} = \frac{1}{12}(BH^3 - bh^3)$
$\bar{I} = \frac{1}{12}[ \, 8(8^3) - 4(4^3) \, ]$
$\bar{I} = 320 \, \text{ in.}^4$
$\bar{I}_x = \bar{I}_y = \bar{I}$
$\bar{I}_x = \bar{I}_y = 320 \, \text{ in.}^4$
Area
$A = 8^2 - 4^2$
$A = 48 \, \text{ in.}^2$
By transfer formula for moment of inertia
$I = \bar{I} + Ad^2$
$I = 320 + 48(4^2)$
$I = 1088 \, \text{ in.}^4$
$I_x = I_y = I$
$I_x = I_y = 1088 \, \text{ in.}^4$
Polar moment of inertia
$J = I_z = I_x + I_y$
$J = 1088 + 1088$
$J = 2176 \, \text{ in.}^4$ answer
Radius of gyration
$k_z = \sqrt{\dfrac{J}{A}} = \sqrt{\dfrac{2176}{48}}$
$k_z = 6.733 \, \text{ in.}$ answer
