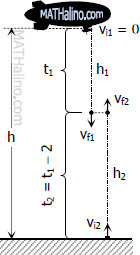
$h = 304.8 \, \text{ m}$
$v_{i2} = 75.6 \, \text{ m/s}$
$g = 9.75 \, \text{ ft/s}^2$
Stone dropped from captive balloon (free-falling body):
$h_1 = \frac{1}{2}gt^2 = \frac{1}{2}(9.75){t_1}^2$
$h_1 = 4.875{t_1}^2$
Stone thrown vertically from the ground 2 seconds later
$s = v_{i2}t_2 - \frac{1}{2}g{t_2}^2$
$h_2 = 75.6t_2 - \frac{1}{2}(9.75){t_2}^2$
$h_2 = 75.6(t_1 - 2) - 4.875(t_1 - 2)^2$
$h_1 + h_2 = h$
$4.875{t_1}^2 + [ \, 75.6(t_1 - 2) - 4.875(t_1 - 2)^2 \, ] = 304.8$
$4.875{t_1}^2 + 75.6(t_1 - 2) - 4.875({t_1}^2 - 4t_1 + 4) = 304.8$
$4.875{t_1}^2 + 75.6t_1 - 151.2 - 4.875{t_1}^2 + 19.5t_1 - 19.5 = 304.8$
$4.875{t_1}^2 + 75.6t_1 - 151.2 - 4.875{t_1}^2 + 19.5t_1 - 19.5 = 304.8$
$95.1t_1 = 475.5$
$t_1 = 5 \, \text{ sec}$
The stones will pass each other 5 seconds after the first stone was dropped from the captive balloon. answer
$h_2 = 75.6(5 - 2) - 4.875(5 - 2)^2$
$h_2 = 182.925 \, \text{ m}$
The stones will meet at a point 182.925 m above the ground. answer
