Spherical Sector

A spherical sector is a solid generated by revolving a sector of a circle about an axis which passes through the center of the circle but which contains no point inside the sector. If the axis of revolution is one of the radial sides, the sector thus formed is spherical cone; otherwise, it is open spherical sector.
 

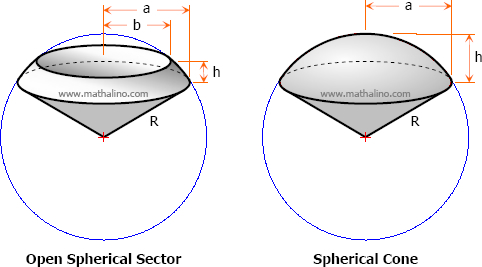
Open Spherical Sector and Spherical Cone

 

Properties of Spherical Sector

  • Spherical sector is bounded by a zone and one or two conical surfaces.
  • The spherical sector having only one conical surface is called a spherical cone, otherwise it is called open spherical sector.
  • The base of spherical sector is its zone.

 
Formulas for Spherical Sector

Total surface area, A
The total surface area of a spherical sector is equal to the area of the zone plus the sum of the lateral areas of the bounding cones.

Total surface area = Zone + Lateral area of bounding cones

$A = A_{zone} + A_1 + A_2$

$A = 2\pi Rh + \pi aR + \pi bR$

$A = \pi R(2h + a + b)$

 

Note that for spherical cone, b = 0 and the equation will reduce to

$A = \pi R(2h + a)$

 

Volume, V
The volume of spherical sector, either open spherical sector or spherical cone, is equal to one-third of the product of the area of the zone and the radius of the sphere. This is similar to the volume of a cone which is Vcone = 1/3 Abh. In spherical sector, replace Ab with Azone and h with R.

$V = \frac{1}{3} A_{zone} R$

$V = \frac{2}{3} \pi R^2 h$