The Prismatoid and the Prismoidal Formula
The General Prismatoid
A general prismatoid is a solid such that the area of any section, say Ay, parallel to and distant y from a fixed plane can be expressed as a polynomial of y of degree not higher than the third.
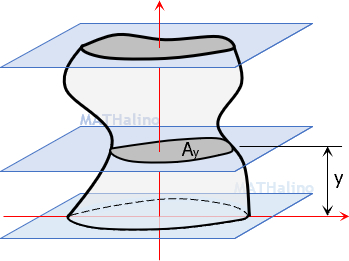
A solid is a general prismatoid if
Where a, b, c, and d are arbitrary constants which may be positive, negative, or zero.
Prisms and cylinders in general are prismatoids in which Ay is constants. Meaning, the value of b, c, and d are zero.
Cones and pyramids including their frustums are first degree prismatoids, meaning, the value of c and d are zero.
Spheres and segment of spheres are examples of second degree prismatoids.
The Prismatoid
A prismatoid is a polyhedron having bases containing all its vertices in two parallel planes. The lateral faces are triangles or trapezoids or parallelograms with one side lying on one of its two bases.
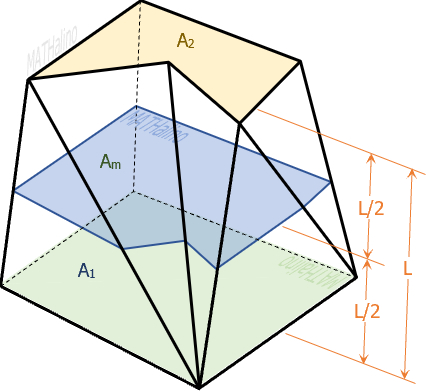
Cubes, cuboids, prisms, pyramids, and pyramidal frustums are examples of basic prismatoids. Prismatoids having vertices equal in numbers in both bases are called Prismoids.
The Prismoidal Formula
The volume of prismatoid is given by this formula:
Where
A1 and A2 = areas of parallel bases
Am = area of the section midway between A1 and A2
L = perpendicular distance between A1 and A2
Note: A solid in which all sections parallel to a certain base are similar figures, is a prismatoid.
