Common Prisms: Cube and Rectangular Parallelepiped
There are two very common prisms; the cube and rectangular parallelepiped. In non-mathematical term, both are called box.
Cube
Cube is one of the Platonic Solids and is called regular hexahedron. It is a polyhedron whose six faces are all squares.
Properties of a Cube
- All edges of a cube are equal in length.
- All faces of the cube are congruent squares.
Formulas for Cube
$V = A_b \, h = a^3$
$A = 6a^2$
$d = a\sqrt{2}$
$s = a\sqrt{3}$
Rectangular Parallelepiped (Cuboid)
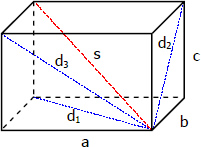All faces of rectangular parallelepiped are rectangles and two opposite faces are equal rectangles.
Properties of Rectangular Parallelepiped
- Parallel edges of rectangular parallelepiped are equal in length.
- Any two opposite faces of rectangular parallelepiped are equal and parallel rectangles.
Formulas for Rectangular Parallelepiped
$V = A_b \, h = abc$
$A = 2(ab + bc + ac)$
$d_1 = \sqrt{a^2 + b^2}$
$d_2 = \sqrt{b^2 + c^2}$
$d_3 = \sqrt{a^2 + c^2}$
$s = \sqrt{a^2 + b^2 + c^2}$
Tags