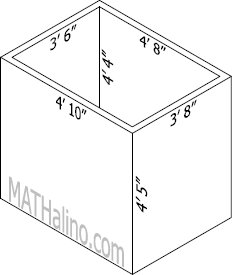
Internal dimensions
$= 4'8'' \text{ by } 3'6'' \text{ by } 4'4''$
External dimensions
$= 4'10'' \text{ by } 3'8'' \text{ by } 4'5''$
Internal volume
$V_i = \left( 4 + \dfrac{8}{12} \right)\left( 3 + \dfrac{6}{12} \right)\left( 4 + \dfrac{4}{12} \right)$
$V_i = \dfrac{637}{9} \, \text{ ft}^3$
External volume
$V_e = \left( 4 + \dfrac{10}{12} \right)\left( 3 + \dfrac{8}{12} \right)\left( 4 + \dfrac{5}{12} \right)$
$V_e = \dfrac{16\,907}{216} \, \text{ ft}^3$
Volume of sheet iron
$V = V_e - V_i$
$V = \dfrac{16\,907}{216} - \dfrac{637}{9}$
$V = \dfrac{1619}{216} \, \text{ ft}^3$
Unit weight of salt water
$\gamma_{sea} = 64 \, \text{ lb/ft}^3$
Unit weight of iron
$\gamma_{iron} = 7.2 \, \gamma_{sea}$
$\gamma_{iron} = 7.2(64)$
$\gamma_{iron} = 460.8 \, \text{ lb/ft}^3$
Weight of tank when empty
$W_{empty} = \gamma_{iron} V$
$W_{empty} = 460.8 \left( \dfrac{1619}{216} \right)$
$W_{empty} = 3453.87 \, \text{ lb}$ answer
Weight of tank when full of seawater
$W_{full} = W_{empty} + W_{sea}$
$W_{full} = 3453.87 + \gamma_{sea} V_i$
$W_{full} = 3453.87 + 64(637/9)$
$W_{full} = 7983.64 \, \text{ lb}$ answer
