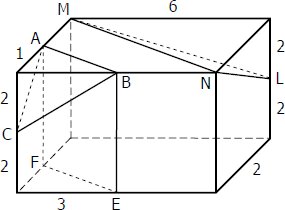
$AB = \sqrt{3^2 + 1^2}$
$AB = \sqrt{10} = EF$
$AC = \sqrt{1^2 + 2^2}$
$AC = \sqrt{5}$
$BC = \sqrt{3^2 + 2^2}$
$BC = \sqrt{13}$
$LN = \sqrt{2^2 + 2^2}$
$LN = 2\sqrt{2}$
$LM = \sqrt{2^2 + 6^2}$
$LM = 2\sqrt{10}$
$MN = \sqrt{2^2 + 6^2}$
$MN = 2\sqrt{10}$
Area of ABEF
$A_{ABEF} = AB \times BE$
$A_{ABEF} = \sqrt{10} \times 4$
$A_{ABEF} = 4\sqrt{10} \, \text{ unit}^2$
For section ABC
$s = \frac{1}{2}(AB + BC + AC)$
$s = \frac{1}{2}(\sqrt{10} + \sqrt{5} + \sqrt{13})$
$s = 4.5019 \, \text{ units}$
$A_{ABC} = \sqrt{s(s - AB)(s - BC)(s - AC)}$
$A_{ABC} = \sqrt{4.5019(4.5019 - \sqrt{10})(4.5019 - \sqrt{5})(4.5019 - \sqrt{13})}$
$A_{ABC} = 3.5 \, \text{ unit}^2$ answer
For section MNL
$s = \frac{1}{2}(LN + LM + MN)$
$s = \frac{1}{2}(2\sqrt{2} + 2\sqrt{10} + 2\sqrt{10})$
$s = 7.7388 \, \text{ units}$
$A_{MNL} = \sqrt{s(s - LN)(s - LM)(s - MN)}$
$A_{MNL} = \sqrt{7.7388(7.7388 - 2\sqrt{2})(7.7388 - 2\sqrt{10})(7.7388 - 2\sqrt{10})}$
$A_{MNL} = 2\sqrt{19} \, \text{ unit}^2 = 8.72 \, \text{ unit}^2$ answer
