The Cylinder
Cylinder is a solid bounded by a closed cylindrical surface and two parallel planes.
Properties of a cylinder
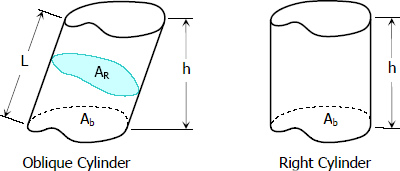
 The bounding cylindrical surface of a cylinder is called the lateral surface, and the two bounding parallel planes are called the bases. The area of the lateral surface is denoted by AL and the area of the base is denoted by Ab.
The bounding cylindrical surface of a cylinder is called the lateral surface, and the two bounding parallel planes are called the bases. The area of the lateral surface is denoted by AL and the area of the base is denoted by Ab.- The bases of a cylinder are equal.
- The altitude of the cylinder is the perpendicular distance between the bases. It is denoted by h.
- Every section parallel to the base is equal to the base.
- Any two parallel sections, neither of which cuts a base are congruent.
- The right section is perpendicular to the axis of the cylinder. The area of the right section is denoted as AR.
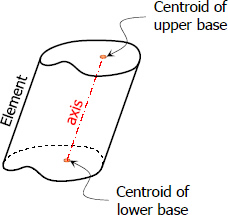
- Axis of the cylinder is the line that connects the centroids of bases. The length of the axis is equal to the length of the element, it is deoted as L.
- For right cylinder, the area of the right section is equal to the area of the base and the length of the axis is equal to the altitude.
Name of a Cylinder
The name of a cylinder is according to the shape of its base. If the base is ellipse, the cylinder is called elliptical cylinder, and if circle, it is called circular cylinder. The most common type of cylinder is the right circular cylinder.
Formulas for Cylinder
$V = A_R \, L = A_b \, h$
$A_L = P_R \, L$
V = volume of the cylinder
AR = area of the right section
L = length of the lateral side
Ab = area of the base
h = altitude
AL = area of the lateral side
PR = perimeter of the base
Note that for right cylinder, AR = Ab and L = h.
Tags
