cylinder
013 Review Problem - Volume of water inside the Venturi meter
Problem 13
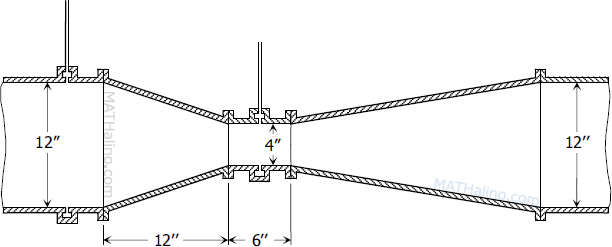
The accompanying figure represents the longitudinal view of a Venturi meter, a device designed to measure the flow of water in pipes. If the throat of the of the meter is 6 in. long and has an inside diameter of 4 in., find the volume of water in the meter which is used in 12-in. pipe line if the altitudes of the tapering parts are in the ratio 1:3 and the smaller altitude measures 12 in.
007 Review Problem - Length of wire
Problem 7
If a piece of brass 8 by 6 by 12 in. is drawn out into a wire 1/30 in. in diameter, what will be the length of the wire?
- Read more about 007 Review Problem - Length of wire
- Log in to post comments
Cylinder of maximum volume and maximum lateral area inscribed in a cone
Situation
A right circular cylinder of radius r and height h is inscribed in a right circular cone of radius 6 m and height 12 m.
Part 1: Determine the radius of the cylinder such that its volume is a maximum.
A. 2 m
B. 4 m
C. 3 m
D. 5 m
Part 2: Determine the maximum volume of the cylinder.
A. 145.72 m3
B. 321.12 m3
C. 225.31 m3
D. 201.06 m3
Part 3: Determine the height of the cylinder such that its lateral area is a maximum.
A. 10 m
B. 8 m
C. 6 m
D. 4 m
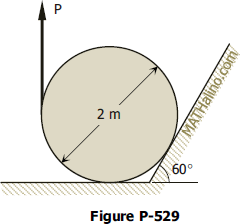
Problem 529 | Friction
Problem 529
As shown in Fig. P-529, a homogeneous cylinder 2 m in diameter and weighing 12 kN is acted upon by a vertical force P. Determine the magnitude of P necessary to start the cylinder turning. Assume that μ = 0.30.
- Read more about Problem 529 | Friction
- 1 comment
- Log in to post comments
Problem 527 and Problem 528 | Friction
Problem 527
A homogeneous cylinder 3 m in diameter and weighing 30 kN is resting on two inclined planes as shown in Fig. P-527. If the angle of friction is 15° for all contact surfaces, compute the magnitude of the couple required to start the cylinder rotating counterclockwise.

Problem 528
Instead of a couple, determine the minimum horizontal force P applied tangentially to the left at the top of the cylinder described in Prob. 527 to start the cylinder rotating counterclockwise.
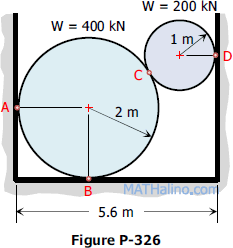
Problem 326 | Equilibrium of Force System
Problem 326
The cylinders in Fig. P-326 have the indicated weights and dimensions. Assuming smooth contact surfaces, determine the reactions at A, B, C, and D on the cylinders.
- Read more about Problem 326 | Equilibrium of Force System
- Log in to post comments
Problem 319 | Equilibrium of Concurrent Force System
Problem 319
Cords are loop around a small spacer separating two cylinders each weighing 400 lb and pass, as shown in Fig. P-319 over a frictionless pulleys to weights of 200 lb and 400 lb . Determine the angle θ and the normal pressure N between the cylinders and the smooth horizontal surface.

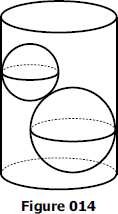
015 Two unequal balls inside the cylinder
Example 015
Two balls, one 15 cm in diameter and the other 10 cm in diameter, are placed in a cylindrical jar 20 cm in diameter, as shown in Figure 014. Find the volume of water necessary to cover them.
- Read more about 015 Two unequal balls inside the cylinder
- Log in to post comments