The Right Circular Cylinder

Tags: 
altitude
cylinder
lateral area
volume
area of the base
axis of cylinder
circular cylinder

A right circular cylinder is a cylinder whose base is a circle and whose elements are perpendicular to its base.
 

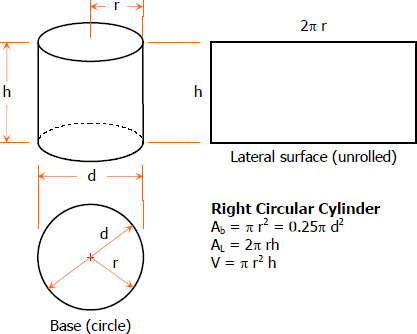
Right Circular Cylinder Exploded

 

Properties of a Right Circular Cylinder

  1. The axis of a right circular cylinder is the line joining the centers of the bases.
  2. For any oblique or non-oblique sections which do not pass any one base, the center of which is at the axis.
  3. A right circular cylinder can be formed by revolving a rectangle about one side as axis of revolution.
  4. Every section of a right circular cylinder made by a cutting plane containing two elements and parallel to the axis is a rectangle.

 

Formulas for Right Circular Cylinder

Area of the base, Ab
$ A_b = \pi r^2 $

$ A_b = \dfrac{\pi}{4}d^2 $

 

Lateral Area, AL
$ A_L = 2\pi \, rh $

$ A_L = \pi \, dh $

 

Volume, V
$ V = A_b h $

$ V = \pi r^2 h $

$ V = \dfrac{\pi}{4} d^2 h $

 

Total Area, AT
Total area (open both ends), $ A_T = A_L $

Total Area (open one end), $ A_T = A_b + A_L $

Total Area (closed both ends), $ A_T = 2A_b + A_L $

 

»
SPONSORED LINKS


Page copy protected against web site content infringement by Copyscape

Recent comments