The Prism
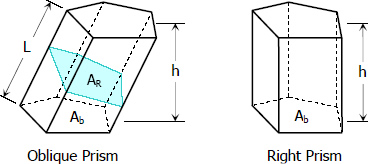
Prism is a polyhedron in which two faces are equal polygons in parallel planes, and all other faces are parallelograms. There are two types of prism; oblique prism and right prism. Oblique prism is when the axis is not perpendicular to the base and right prism if the axis is parallel to the base. In right prism, all lateral areas are rectangle.
Formulas
$V = A_b \, h$
V = volume of the prism
AR = area of the right section
L = length of the lateral side
Ab = area of the base
h = altitude
AL = area of the lateral side
PR = perimeter of the right section
Note that for right prism, AR = Ab and L = h.
Name of a Prism
The name of a prism is according to the shape its base and according to the orientation of the axis. The naming according to orientation of the axis is specifically used for right prism. Example, if the base of the prism is a pentagon like the figure above, it is called pentagonal prism. If the base is a regular pentagon, then the name of the prism is regular pentagonal prism. If the shape of the base is a regular pentagon and the axis of the prism is perpendicular to the base, the prism is called right regular pentagonal prism. However, if the problem will just mention pentagonal prism without specifying regular pentagon or right, it is most of the time a right regular pentagonal prism.
Elements of a Prism
Prism has two equal parallel bases, the upper and lower base. The area of the base is denoted by Ab.
The perpendicular distance distance between the upper and lower bases and is denoted by h.
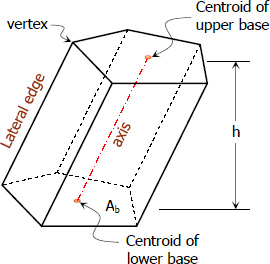
The line that connects the centroid of upper and lower bases. The length of axis is equal to the length of the lateral edge.
Lateral are or lateral side is a line that connects the corresponding vertices of the bases. Edge in general is the line made by the intersection of two faces. Lateral edge is the line formed by the intersection of two lateral faces.
Area of the side of the prism, it is denoted by AL.
Right section is the section made by a cutting plane that is perpendicular to the axis of the prism. The area of the right section is denoted by AR.
Vertex is a point formed by the intersection of three or more edges. Note that at least three edges must intersect to define the vertex of a solid.
