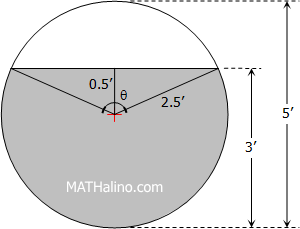
$\cos \frac{1}{2}\theta = \dfrac{0.5}{2.5}$
$\frac{1}{2}\theta = 78.463^\circ$
$\theta = 156.926^\circ$
$\alpha = 360^\circ - \theta = 360^\circ - 156.926^\circ$
$\alpha = 203.074^\circ$
Area of cross section:
$A_b = \frac{1}{2} r^2(\alpha_{rad} + \sin \theta_{deg})$
$A_b = \frac{1}{2} (2.5^2)\left( 203.074^\circ \cdot \dfrac{\pi}{180^\circ} + \sin 156.926^\circ \right)$
$A_b = 12.3 ~ \text{ft}^2$
Volume of water:
$V_w = A_b L = 12.3(12)$
$V_w = 147.61 ~ \text{ft}^3$
Depth of water in vertical position:
$V_w = \pi r^2 h$
$147.61 = \pi (2.5^2)h$
$h = 7.518 ~ \text{ft}$ answer
