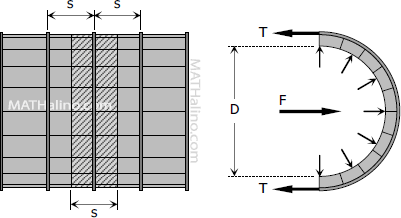
Stresses on Thin-walled Pressure Tanks
The circumferential stress, also known as tangential stress, in a tank or pipe can be determined by applying the concept of fluid pressure against curved surfaces. The wall of a tank or pipe carrying fluid under pressure is subjected to tensile forces across its longitudinal and transverse sections.
- Read more about Stresses on Thin-walled Pressure Tanks
- Log in to post comments