Stresses on Thin-walled Pressure Tanks

The circumferential stress, also known as tangential stress, in a tank or pipe can be determined by applying the concept of fluid pressure against curved surfaces. The wall of a tank or pipe carrying fluid under pressure is subjected to tensile forces across its longitudinal and transverse sections.
 

Tangential Stress, σ_t (Circumferential Stress)
Consider the tank shown being subjected to an internal pressure p. The length of the tank is L perpendicular to the drawing and the wall thickness is t. Isolating the right half of the tank:
 

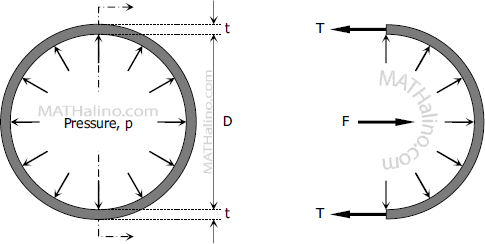
$2T = F$

$2(\sigma_t tL) = pDL$

$2t\sigma_t = pD$

Longitudinal Stress, σ_l
At the end of the tank, the total stress P_T = σ_l A_end should equal the total fluid force F at that end. Since the wall thickness t is so small compared to internal diameter D, the area A_end of the wall is close to πDt.
 

$P_T = F$

$\sigma_lA_{end} = \pi A_i$

$\sigma_l(\pi Dt) = p(\frac{1}{4}\pi D^2)$

$t\sigma_l = \frac{1}{4}p D$

Observe that the tangential stress is twice that of the longitudinal stress.

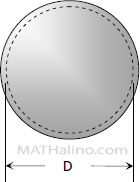
Spherical Shell
If a spherical tank of diameter D and thickness t contains gas under a pressure of p, the stress at the wall can be expressed as:
 

Spacing of Hoops of Wood Stave Vessels
It is assumed that the wood will not resist tension, only the hoops will resist all the tensile stress caused by the internal pressure p.
 

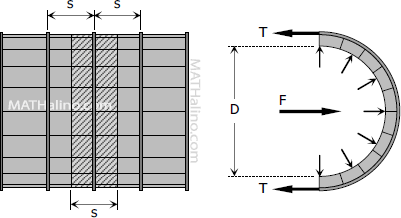
$F = 2T$

$pDs = 2 \sigma_t A_h$

where
s = spacing of hoops
σ_t = allowable tensile stress of the hoop
A_h = cross-sectional area of the hoop
p = internal pressure in the vessel
D = internal diameter of the vessel