Total Hydrostatic Force on Surfaces

Total Hydrostatic Force on Plane Surfaces

For horizontal plane surface submerged in liquid, or plane surface inside a gas chamber, or any plane surface under the action of uniform hydrostatic pressure, the total hydrostatic force is given by
 

where p is the uniform pressure and A is the area.
 

In general, the total hydrostatic pressure on any plane surface is equal to the product of the area of the surface and the unit pressure at its center of gravity.
 

where p_cg is the pressure at the center of gravity. For homogeneous free liquid at rest, the equation can be expressed in terms of unit weight γ of the liquid.
 

where   $\bar{h}$   is the depth of liquid above the centroid of the submerged area.
 

Derivation of Formulas
The figure shown below is an inclined plane surface submerged in a liquid. The total area of the plane surface is given by A, cg is the center of gravity, and cp is the center of pressure.
 

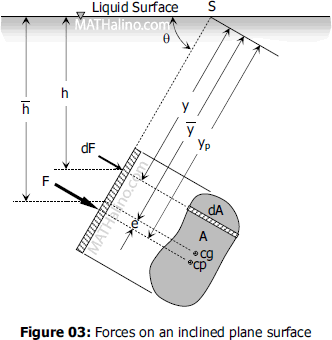
The differential force dF acting on the element dA is
$dF = p \, dA$

$dF = \gamma h \, dA$
 

From the figure   $h = y \sin \theta$,
$dF = \gamma(y \sin \theta) \, dA$
 

Integrate both sides and note that γ and θ are constants,
$\displaystyle F = \gamma \sin \theta \int y \, dA$
 

Recall from Calculus that   $\displaystyle \int y \, dA = A\bar{y}$
$F = (\gamma \sin \theta) A\bar{y}$

$F = \gamma (\bar{y} \sin \theta)A$
 

From the figure,   $\bar{y} \sin \theta = \bar{h}$,   thus,

The product   $\gamma \bar{h}$   is a unit pressure at the centroid at the plane area, thus, the formula can be expressed in a more general term below.

Location of Total Hydrostatic Force (Eccentricity)
From the figure above, S is the intersection of the prolongation of the submerged area to the free liquid surface. Taking moment about point S.

$\displaystyle Fy_p = \int y \, dF$

$\displaystyle [ \, \gamma (\bar{y} \sin \theta)A \, ]y_p = \int y \, [ \, \gamma(y \sin \theta) \, dA \, ]$

$\displaystyle (\gamma \sin \theta) A \bar{y} \, y_p = (\gamma \sin \theta) \int y^2 \, dA$

$\displaystyle A \bar{y} \, y_p = \int y^2 \, dA$
 

Again from Calculus,   $\displaystyle \int y^2 \, dA$   is called moment of inertia denoted by I Since our reference point is S,

$A \bar{y} \, y_p = I_S$
 

Thus,

By transfer formula for moment of inertia   $I_S = I_g + A{\bar{y}}^2$,   the formula for y_p will become   $y_p = \dfrac{I_g + A{\bar{y}}^2}{A \bar{y}}$   or

From the figure above,   $y_p = \bar{y} + e$,   thus, the distance between cg and cp is

Total Hydrostatic Force on Curved Surfaces

In the case of curved surface submerged in liquid at rest, it is more convenient to deal with the horizontal and vertical components of the total force acting on the surface. Note: the discussion here is also applicable to plane surfaces.
 

Horizontal Component
The horizontal component of the total hydrostatic force on any surface is equal to the pressure on the vertical projection of that surface.

Vertical Component
The vertical component of the total hydrostatic force on any surface is equal to the weight of either real or imaginary liquid above it.

Total Hydrostatic Force

Direction of   $F$

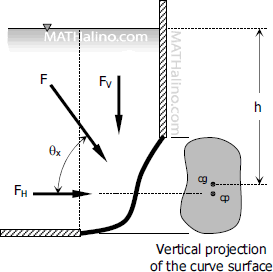
Case 1: Liquid is above the curve surface
The vertical component of the hydrostatic force is downward and equal to the volume of the real liquid above the submerged surface.
 

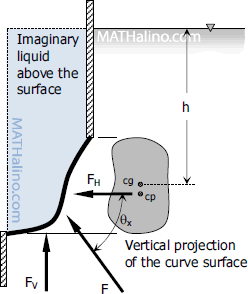
Case 2: Liquid is below the curve surface
The vertical component of the hydrostatic force is going upward and equal to the volume of the imaginary liquid above the surface.