Buoyancy

Archimedes Principle

Archimedes (287-212 B.C.)

Any body immersed in a fluid is subjected to an upward force called buoyant force equal to the weight of the displaced fluid.

$BF = \gamma V_D$

Where
$BF$ = buoyant force
$\gamma$ = unit weight of fluid
$V_D$ = volume of fluid displaced by the body

Buoyant force acting on a body submerged in fluid is merely the resultant of two vertical hydrostatic forces. Consider the cylindrical body shown below to have some length perpendicular to the drawing. The horizontal components of hydrostatic force acting on the body are in equilibrium because the vertical projection of the body in opposite sides is the same.

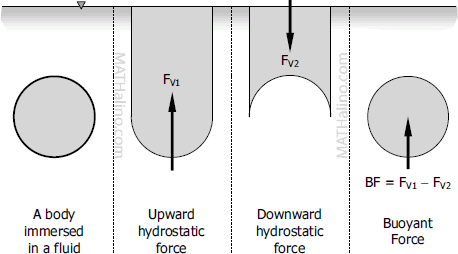
The upward force $F_{V1}$ is the total force exerted by the fluid on the under surface of the body; the downward force $F_{V2}$ is the total force exerted by the fluid on the upper surface of the body. Since liquid pressure increases by depth, $F_{V1}$ is greater than $F_{V2}$. The difference $F_{V1} - F_{V2}$ is therefore upward, and this difference is the buoyant force.

For homogeneous body of volume $V$ "floating" in a homogeneous liquid at rest, the volume displaced is

$V_D = \dfrac{sg_{body}}{sg_{fluid}}V = \dfrac{\gamma_{body}}{\gamma_{fluid}}V$

For a floating body of height $H$ and constant cross-sectional area parallel to the liquid surface, the submerged length $D$ is given by

$D = \dfrac{sg_{body}}{sg_{fluid}}H = \dfrac{\gamma_{body}}{\gamma_{fluid}}H$

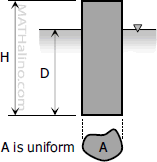
For a floating body whose cross-sectional area $A$ is perpendicular to the liquid surface, the area submerged is given by

$A_s = \dfrac{sg_{body}}{sg_{fluid}}A = \dfrac{\gamma_{body}}{\gamma_{fluid}}A$

Navigation

Recent comments