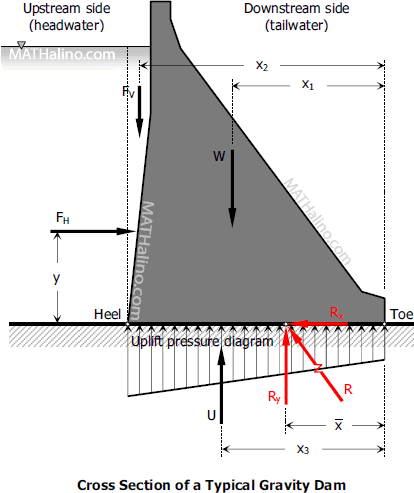
Analysis of Gravity Dam
Dams are structures whose purpose is to raise the water level on the upstream side of river, stream, or other waterway. The rising water will cause hydrostatic force which will tend the dam to slide horizontally and overturn about its downstream edge or toe. The raised water level on the upstream edge or heel will also cause the water to seep under the dam. The pressure due to this seepage is commonly called hydrostatic uplift and will reduce the stability of the dam against sliding and against overturning.
Gravity Dam Analysis
The weight of gravity dam will cause a moment opposite to the overturning moment and the friction on the base will prevent the dam from sliding. The dam may also be prevented from sliding by keying its base into the bedrock.
Step 1
Consider 1 unit length (1 m length) of dam perpendicular to the cross section.
Step 2
Determine all the forces acting:
- Vertical forces
- $W$ = Weight of dam
- $F_V$ = Weight of water in the upstream side (if any)
- $U$ = Hydrostatic uplift
- Weight of permanent structures on the dam
- Horizontal forces
- $F_H$ = Horizontal component of total hydrostatic force
- Wind pressure, wave action, floating bodies, earthquake load, etc.
Step 3
Solve for the reaction
- Horizontal component of the reaction
$R_x = \Sigma F_H$ - Vertical component of the reaction
$R_y = \Sigma F_V$
Step 4
Moment about the toe
- Righting moment, $RM$
$RM$ = Sum of all rotation towards the upstream side - Overturning moment, $OM$
$OM$ = Sum of all rotation towards the downstream side
Step 5
Location of $R_y$ as measured from the toe
Factors of Safety
Factor of safety against sliding, $FS_s$
Factor of safety against overturning, $FS_o$
Where $\mu$ = coefficient of friction between the base of the dam and the foundation.
Foundation Pressure
Eccentricity, $e$
If $e \le B/6$, $R_y$ is within the middle third and the foundation pressure is trapezoidal acting from heel to toe. If $e$ is exactly $B/6$, the shape of foundation pressure is triangular also acting from heel to toe.
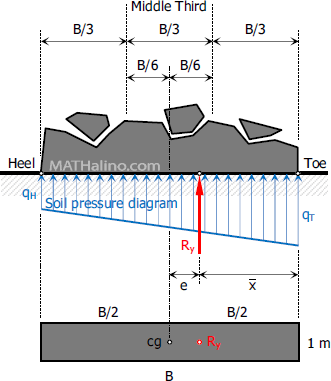
For the sign of $6e/B$, use (+) at point where $R_y$ is nearest. From the diagram above, use (+) for $q_T$ and (-) for $q_H$. A negative $q$ indicates compressive stress and a positive $q$ indicates tensile stress. A positive $q$ will occur when $e > B/6$. In foundation design, soil is not allowed to carry tensile stress, thus, any $+q$ will be neglected in the analysis.
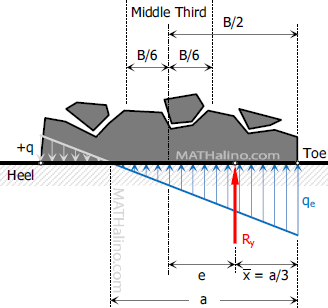
If $e > B/6$, $R_y$ is outside the middle third and the foundation pressure is triangular.
- Log in to post comments
