inclined plane

Total Hydrostatic Force on Plane Surfaces
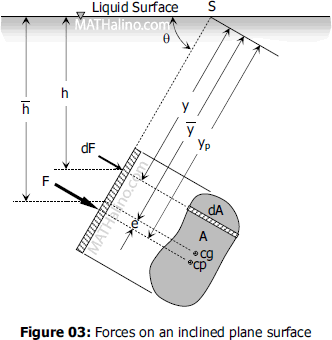
For horizontal plane surface submerged in liquid, or plane surface inside a gas chamber, or any plane surface under the action of uniform hydrostatic pressure, the total hydrostatic force is given by
 

where p is the uniform pressure and A is the area.
 

In general, the total hydrostatic pressure on any plane surface is equal to the product of the area of the surface and the unit pressure at its center of gravity.
 

where p_cg is the pressure at the center of gravity. For homogeneous free liquid at rest, the equation can be expressed in terms of unit weight γ of the liquid.
 

where   $\bar{h}$   is the depth of liquid above the centroid of the submerged area.
 

Problem 01
A projectile is fired up the inclined plane at an initial velocity of 15 m/s. The plane is making an angle of 30° from the horizontal. If the projectile was fired at 30° from the incline, compute the maximum height z measured perpendicular to the incline that is reached by the projectile. Neglect air resistance.
 

Problem 529
As shown in Fig. P-529, a homogeneous cylinder 2 m in diameter and weighing 12 kN is acted upon by a vertical force P. Determine the magnitude of P necessary to start the cylinder turning. Assume that μ = 0.30.
 

Problem 527
A homogeneous cylinder 3 m in diameter and weighing 30 kN is resting on two inclined planes as shown in Fig. P-527. If the angle of friction is 15° for all contact surfaces, compute the magnitude of the couple required to start the cylinder rotating counterclockwise.
 

Problem 528
Instead of a couple, determine the minimum horizontal force P applied tangentially to the left at the top of the cylinder described in Prob. 527 to start the cylinder rotating counterclockwise.
 

Problem 522
The blocks shown in Fig. P-522 are separated by a solid strut which is attached to the blocks with frictionless pins. If the coefficient of friction for all surfaces is 0.20, determine the value of horizontal force P to cause motion to impend to the right. Assume that the strut is a uniform rod weighing 300 lb.
 

Problem 514
The 10-kN cylinder shown in Fig. P-514 is held at rest on the 30° incline by a weight P suspended from a cord wrapped around the cylinder. If slipping impends, determine P and the coefficient of friction.
 

Problem 513
In Fig. P-512, the homogeneous block weighs 300 kg and the coefficient of friction is 0.45. If h = 50 cm, determine the force P to cause motion to impend.
 

Problem 512
A homogeneous block of weight W rests upon the incline shown in Fig. P-512. If the coefficient of friction is 0.30, determine the greatest height h at which a force P parallel to the incline may be applied so that the block will slide up the incline without tipping over.
 

Problem 509
The blocks shown in Fig. P-509 are connected by flexible, inextensible cords passing over frictionless pulleys. At A the coefficients of friction are μ_s = 0.30 and μ_k = 0.20 while at B they are μ_s = 0.40 and μ_k = 0.30. Compute the magnitude and direction of the friction force acting on each block.
 

Problem 508
The 200-lb block shown in Fig. P-508 has impending motion up the plane caused by the horizontal force of 400 lb. Determine the coefficient of static friction between the contact surfaces.