01 Area of a right triangle of known median bisecting the hypotenuse
Problem
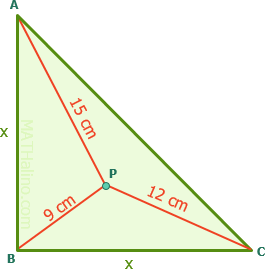
The median of a right triangle drawn to the hypotenuse is 3 cm long and makes an angle of 60° with it. Find the area of the triangle.
| A. 7.97 cm2 | C. 8.79 cm2 |
| B. 8.97 cm2 | D. 7.79 cm2 |